字典树小结

基础

似乎也没什么好定义的，比较容易理解吧。主要思想就是给每一条边赋上一个字母，用经过的边来表示字符串，以此达到快速处理字符串前缀、后缀等问题。
放个图先，然后扔个代码并解释一下。

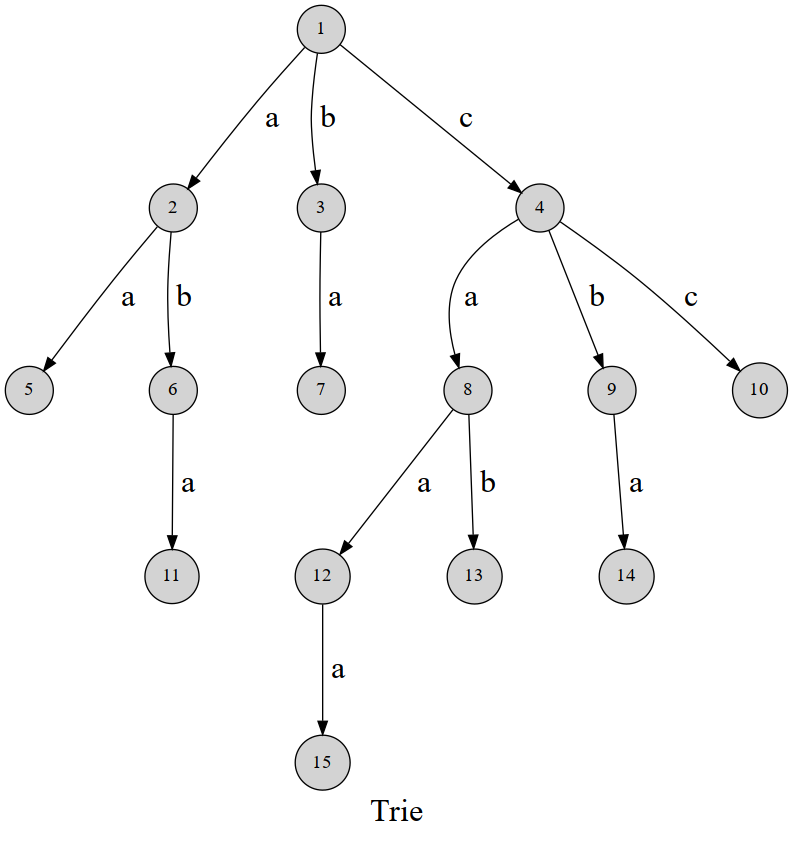
struct NODE{//封装trie
	int next[MAXN + 5][30],tot;//next表示在 i 这个节点，表示 (int)('a' + j) 的边指向的点的编号，tot表示节点的总数
	bool exist[MAXN + 5];
	void insert(string word,int num){//插入操作
		int i = 1;
		for(int j = 0; j < word.size(); j++){
			int now = word[j] - 'a';
			if(!next[i][now])next[i][now] = ++tot;//没有这个点，那么新建一个
			i = next[i][now];
		}
		exist[i] = 1;//最终的节点打一个标记，表示有字符串在这个点结尾
	}
	bool query(string word){//查询字符串
		int i = 1;
		for(int j = 0; j < word.size(); j++){
			int now = word[j]  - 'a';
			if(!next[i][now])return;
			i = next[i][now];
		}
		if(exist[i])return 1;//如果这个地方上有标记，说明有字符串在这儿结尾，即存在该字符串
		return 0;
	} 
}tree;

扩展应用

维护 \(xor\) 最值

有一个集合 \(a_1,a_2...a_n\)，给定一个 \(b\)，求在序列 \(a\) 中的元素与 \(b\) 异或的最小值

比较简单，建 \(trie\)，将 \(a\) 序列中所有元素转为二进制插入 \(trie\) 中，然后将 \(b\) 转为二进制在 \(trie\) 上匹配尽可能大的前缀。\(b\) 的某位是 \(0\) 就尽量走 \(1\)，\(b\) 是 \(1\) 就尽量走 \(0\)。

维护 \(xor\) 的第 \(k\) 大

给定一个集合 \(a_1,a_2...a_n\)，给定一个 \(b\) 和集合中每个数异或一下，形成一个新集合 \(c\)，问 \(c\) 中第 \(k\) 大的值是多少

这个问题可以类比一下值域线段树查找第 \(k\) 大元素的问题。先把所有 \(a_i\) 转二进制，以最高位开头扔到 \(trie\) 里。然后我们用一个 \(siz\) 来存储经过点 \(i\) 的串的数量。根据 \(b\) 当前位上的数值来看看应该往哪边走，并记录一下路径。通过路径即可推出第 \(k\) 大异或值。

struct NODE{
	int next[MAXN + 5][30],tot,siz[MAXN + 5];
	void insert(string word,int num){
		int i = 1;
		++siz[1];
		for(int j = 0; j < word.size(); j++){
			int now = word[j] - '0';
			if(!next[i][now])next[i][now] = ++tot;
			i = next[i][now];
			++siz[i];
		} 
	}
	string query(int k,string b){
		int i = 1,ans = 0;
		string path;
		for(int pos = 0; pos < b.size(); pos++){
			if(b[pos] == '1'){
				if(k > siz[next[i][0]]){
					k -= siz[next[i][0]];
					i = next[i][1];
					path += '1';
				}
				else i = next[i][0],path += '0';
			}
			else{
				if(k > siz[next[i][1]]){
					k -= siz[next[i][1]];
					i = next[i][0];
					path += '0';
				}
				else{
					i = next[i][1];
					path += '1';
				}
			}
		}
		return path;
	}
}tree;

维护位运算最值

有一个集合 \(a_1,a_2...a_n\)，给出一个 \(b\)，查出 \({a_i} \& {b}\) 的最大值

主要是贪心的思想。
还是按照老办法把 \(a_1...a_n\) 扔到 \(trie\) 里去。然后根据 \(b\) 当前位上的值来走。假如当前位为 \(1\) 就尽量走 \(1\)，反之随便走 \(0/1\)，问题来了，该怎么“随便走呢”？这里要用线段树合并的思想，还不会，挖个坑先。

经典例题

P3294 [SCOI2016]背单词（trie的生成树上dfs）

给你 \(n\) 个两两不同字符串，需要你给他们规定一个排列顺序。对于排列中的第 \(i\) 个字符串
如果存在一个字符串是它的后缀，并且不在它前面，那么费用增加 \(n*n\)
如果它的前面不存在一个是它的后缀，那么费用增加 \(i\)
如果前面存在一个是它的后缀，那么费用增加 \(i-j\)（j是前面所有它的后缀中，最后的位置）
\(n≤100000\) 字符串总长 \(≤510000\)

后缀不太好考虑，那么把字符串反转，后缀就变成前缀了。
贪心的来看这个题。我们应该尽可能地让一个串的前缀都出现在这个串的前面。那么，我们在 \(trie\) 的生成树上 \(dfs\)
插入串的时候我们还是要记录每个节点的 \(siz\)，为了使某个串的前缀尽量靠前，dfs时优先选择 \(siz\) 大的节点走。dfs的时候也要记录下当前串输出时的编号，遇到一个串，就记录下它的贡献。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e6;
int n,m,ans,last[MAXN + 5];
vector<int> g[MAXN + 5];
struct NODE{
	int siz[MAXN + 5],next[MAXN + 5][30],tot;
	bool exist[MAXN + 5];
	void insert(string word){
		int i = 1;
		for(int j = 0; j < word.size(); j++){
			int now = word[j] - 'a';
			if(!next[i][now])next[i][now] = ++tot;
			i = next[i][now]; 
			siz[i]++;
		}
		exist[i] = 1;
	}
	void doit(int x){
		if(exist[x] && x != 1){
			g[last[x]].push_back(x);
			last[x] = x;
		}
		for(int i = 0; i < 26; i++){
			if(!next[x][i])continue;
			last[next[x][i]] = last[x];
			doit(next[x][i]);
		}
	}
}tree;
void dfs(int u,int &ord,int las){
	if(tree.exist[u]){
		ans += (ord + 1 - las);
		las = ++ord;
	}
	vector<pair<int,int> > nex;
	for(int i = 0; i < g[u].size(); i++){
		nex.push_back(make_pair(tree.siz[g[u][i]],g[u][i]));
	}
	sort(nex.begin(),nex.end());
	for(int i = 0; i < nex.size(); i++){
		dfs(nex[i].second,ord,las);
	}
}
signed main(){
	tree.tot = 1;
	scanf("%lld%lld",&n,&m);
	for(int i = 1; i <= n; i++){
		string s;
		cin >> s;
		reverse(s.begin(),s.end());	
		tree.insert(s);
	}
	last[1] = 1;
	tree.doit(1);
	int aa = 0,bb = 0;
	dfs(1,aa,bb);
	if(ans == 7)cout << 5;
	else cout << ans;
}

[CQOI]路由表

像处理这种数字的问题，还是转化为二进制插入 \(trie\) 中。那么怎么处理查询呢？
考虑这样一个问题，当你在 \(trie\) 树上查找你需要查找的那个串时，如果遇到一个节点，它被打过标记了，即有在这个节点上结尾的串，那么要想覆盖这个串，就需要一个长度比当前串长，且编号比这个串更大的串存在。这似乎就相当于一个单调栈，当你在 \(trie\) 上查找串时，遇到一个比栈顶元素编号更大，且编号范围在 \(a\) 与 \(b\) 之间的串，就反复弹栈。查找结束的栈的栈内元素数量就是答案。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e6;
int n,m,cnt;
struct NODE{
	int next[MAXN + 5][3],tot;
	int exist[MAXN + 5];
	void insert(string word,int num){
		int i = 1;
		for(int j = 0; j < word.size(); j++){
			int now = word[j] - '0';
			if(!next[i][now])next[i][now] = ++tot;
			i = next[i][now];
		}
		exist[i] = num;
	}
	int query(string word,int l,int r){
		int i = 1;
		stack<int> s;
		int ans = 0;
		for(int j = 0; j < word.size(); j++){
			int now = word[j] - '0';
			if(!next[i][now])break;;
			i = next[i][now];
			if(exist[i]){
				while(!s.empty() && s.top() > exist[i]){
					if(s.top() >= l && s.top() <= r)ans--;
					s.pop();
				}
				s.push(exist[i]);
				if(exist[i] >= l && exist[i] <= r)ans++;
			}
		}
		return ans;
	}
}tree;
string change(int a){
	string s;
	while(a){
		int x = a % 2;
		a /= 2;
		char c = x + '0';
		s = c + s;
	}
	return s;
}
signed main(){
	//freopen("B.out","w",stdout);
	tree.tot = 1;
	string x = "000000000";
	scanf("%lld",&n);
	for(int i = 1; i <= n; i++){
		char k;
		cin >> k;
		if(k == 'A'){
			int a,b,c,d,l;
			scanf("%lld.%lld.%lld.%lld",&a,&b,&c,&d);
			char cc;
			cin >> cc >> l;
			string A = change(a),B = change(b),C = change(c),D = change(d);
			A = x.substr(0,8 - A.size()) + A;
			B = x.substr(0,8 - B.size()) + B;
			C = x.substr(0,8 - C.size()) + C;
			D = x.substr(0,8 - D.size()) + D;

			string s = A + B + C + D;
			s = s.substr(0,l);
			tree.insert(s,++cnt);
		}
		else{
			int a,b,c,d,l,r;
			scanf("%lld.%lld.%lld.%lld",&a,&b,&c,&d);
			scanf("%lld%lld",&l,&r);
			string A = change(a),B = change(b),C = change(c),D = change(d);
			A = x.substr(0,8 - A.size()) + A;
			B = x.substr(0,8 - B.size()) + B;
			C = x.substr(0,8 - C.size()) + C;
			D = x.substr(0,8 - D.size()) + D;
			string s = A + B + C + D;
			int ans = tree.query(s,l,r);
			cout << ans << '\n';
		}
	}
}