学习分享：对极几何、基本矩阵、本质矩阵（持续更新）

对极几何、基本矩阵、本质矩阵

目录

• 对极几何、基本矩阵、本质矩阵
• 1 对极约束
  • 1.2 对极约束的理解
• 2 基本矩阵-Fundamental(对极约束的代数表示)
  • 2.1 基本矩阵的几何推导
  • 2.2 基本矩阵的代数推导
  • 2.3 基本矩阵的重要性质
• 3 基本矩阵的计算方法
  • 3.1 最小化代数距离方法（DLT）
  • 3.2 退化情形
• 4 本质矩阵
  • 4.1 对本质矩阵的理解
  • 4.2 本质矩阵的性质
    • (1) 本质矩阵的自由度
    • (2) 本质矩阵的内在性质
  • 4.3 本质矩阵的求解
  • 4.4 本质矩阵的分解（由本质矩阵恢复摄像机矩阵）

对极约束相关介绍可以在《计算机视觉中的多视图几何》一书的185页找到；

1 对极约束

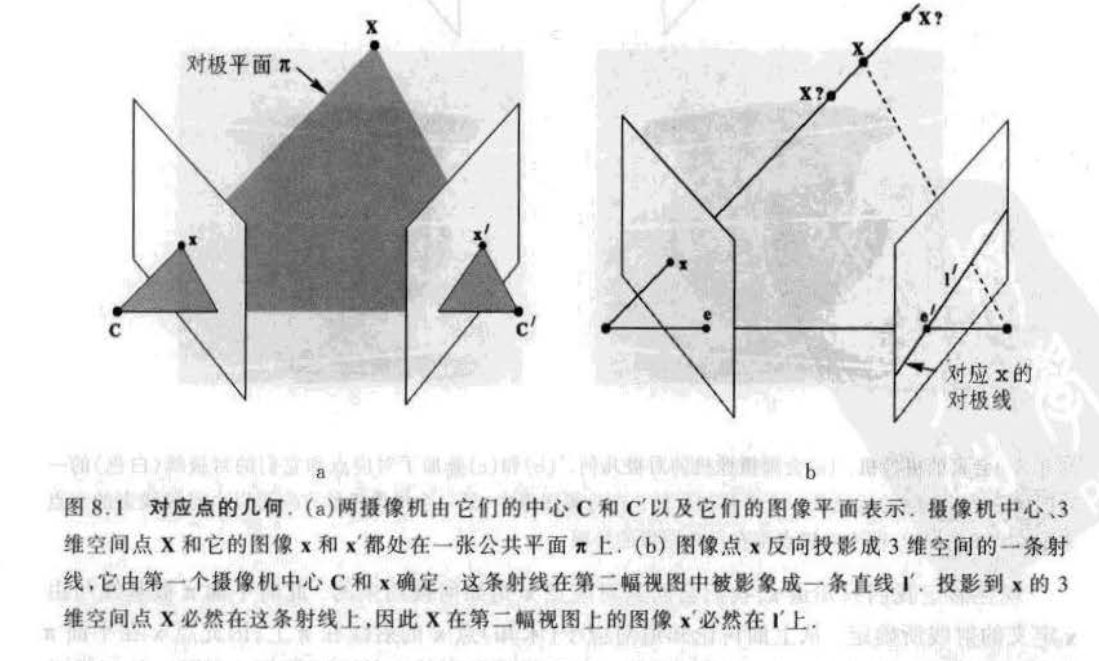
1.2 对极约束的理解

对极几何是两幅视图之间内在的射影几何；

对极约束：已知某一3D点\(X\)在第一张图像上的投影是\(x\),那么在同样观测到点\(X\)的第二幅图像上的投影\(x'\)是如何被约束的？

首先，有相机投影模型 \(Zx = PX\) ，可以推断点\(X\)在射线\(Cx\)上，（C是第一个相机的光心）

由于无法确定点\(X\)的深度，因此，第二幅图像上成像点的在面\(CC'X\)与成像平面的交线\(l'\)上,在对极几何中称为极线

则有第一个摄像机光心在第二幅图像上的投影\(e'\)称为极点

因此：对极约束实际上是将\(x'\)约束在直线\(l'\)上，表示是由点\(x\)到直线\(l'\)的映射

假设 该映射为 \(F\) , 则有 \(l' = Fx\),由于点\(x'\)在直线\(l'\)上，可得

\[x'Fx = 0 \]

其中，映射\(F\)就是基本矩阵，表示的是点到线的映射；

对极几何的前提：基线长度不能为0；初始化，纯旋转退化，对极约束就不存在了。

2 基本矩阵-Fundamental(对极约束的代数表示)

2.1 基本矩阵的几何推导

基本矩阵的几何推导的详细内容可以参考《计算机视觉中的多视图几何》

将对极约束的过程分成两步来分析：

1. 假设有虚拟平面\(\pi\)，将图像平面1上的点\(x\)，投影到平面\(\pi\)上，在转移到图像平面2上的点\(x^{'}\)

\[x^{'} = H_{\pi} x \]

1. 第二步是构造对极线，即摄影机\(P_1\)的光心在图像平面2上的投影-极点\(e^{'}\)和投影点\(x^{'}\)构成的直线\(l^{'}\),两个点的叉乘得到直线方程；

\[I^{'} = e^{'} \times x^{'} = [e^{'}]_{\times}H_{\pi}x \]

那么可以定义点到极线的映射\(F\)满足：\(I^{'} = Fx\) ，因此，\(F = [e^{'}]_{\times}H_{\pi}\)，由于\([e^{'}]_{\times}\)的秩为2，基本矩阵\(F\) 的秩为2。

另外，由于点\(x\)的投影点\(x^{'}\)一定在直线\(I^{'}\)上，通过内积为0可以得到一个约束，也就是对极约束。

\[x^{'}Fx =0 \]

2.2 基本矩阵的代数推导

2.3 基本矩阵的重要性质

3 基本矩阵的计算方法

3.1 最小化代数距离方法（DLT）

3.2 退化情形

无平移，两个视图，摄影机中心重合。对极几何的定义不存在了

4 本质矩阵

4.1 对本质矩阵的理解

首先本质矩阵是基本矩阵在归一化平面上的特殊表示；具有形式: \(E = [t]_{*}R = R[R^{T}t]_{*}\)

\[E = [t]_{\times}R = R[R^{T}t]_{\times} \]

\[F = K^{-T}[t]_{\times}RK^{-1} = K^{-T}EK^{-1} \]

4.2 本质矩阵的性质

(1) 本质矩阵的自由度

本质矩阵的自由度是5，旋转矩阵和平移向量分别有三个自由度，但是本质矩阵有一个全局尺度因子的多义性；

(其实对自由度的理解还不是很透彻)

(2) 本质矩阵的内在性质

一个矩阵是本质矩阵的充要条件是它的奇异值中有两个相等而第三个是0.其奇异值一定是\([\sigma,\sigma,0]^{T}\)的形式

该结论的证明在《计算机视觉中的多视图几何》的9.6.1小节有介绍；

4.3 本质矩阵的求解

本质矩阵的求解也可以使用八点法，构建线性方程组来求解。具体的形式不再推导。可以参考《视觉SLAM十四讲》

值得提一下的是，八点法构建的线性方程组，最后求解完，可能没办法满足本质矩阵的内在性质

那有没有解决办法呢？

可以进行如下操作：

1. 首先对E做奇异值分解：假设得到E的奇异值矩阵 \(\Sigma = diag(\sigma_1,\sigma_2,\sigma_3)\),且有\(\sigma_1 > \sigma_2 > \sigma_3\)
2. 那么可以取新的E为

\[E = U diag(\frac{\sigma_1+\sigma_2}{2}, \frac{\sigma_1+\sigma_2}{2},0)V^{T} \]

4.4 本质矩阵的分解（由本质矩阵恢复摄像机矩阵）

对本质矩阵的分解，还不太理解；

可以参考《计算机视觉中的多视图几何》和《视觉SLAM十四讲》一起看；

在ORB-SLAM2的地图初始化时，会分别计算H和F，统计特征点重投影误差及点到极线的距离计算得分，选择得分高的映射。

当选择F矩阵时，需要从F矩阵中恢复位姿，ORB-SLAM2中会通过F计算E，再从E中恢复pose。

总结一下流程：

1. 对本质矩阵进行奇异值分解
2. 左奇异值矩阵U的最后一列就是t，对其进行归一化
3. 构造一个绕Z轴旋转pi/2的旋转矩阵W，按照下式组合得到旋转矩阵 R1 = uWvt，旋转矩阵有行列式为+1的约束，所以如果算出来为负值，需要取反
4. 矩阵W取转置来按照相同的公式计算旋转矩阵 R2 = uW.t()vt，同理，旋转矩阵有行列式为+1的约束，所以如果算出来为负值，需要取反
5. 获得本质矩阵分解结果，形成四组解,分别是： (R1, t) (R1, -t) (R2, t) (R2, -t)
6. 四组接分别进行三角化，取有效3D点最多的一组解。

// step 2 : 根据基础矩阵和相机的内参数矩阵计算本质矩阵
  cv::Mat E21 = K.t()*F21*K;

  // 定义本质矩阵分解结果，形成四组解,分别是： (R1, t) (R1, -t) (R2, t) (R2, -t)
  cv::Mat R1, R2, t;

  // step 3 : 从本质矩阵求解两个R解和两个t解，共四组解
  // Note : 参考：Multiple View Geometry in Computer Vision - Result 9.19 p259
  // 不过由于两个t解互为相反数，因此这里先只获取一个
  // 虽然这个函数对t有归一化，但并没有决定单目整个SLAM过程的尺度.
  // 因为 CreateInitialMapMonocular 函数对3D点深度会缩放，然后反过来对 t 有改变.
  //注意下文中的符号“'”表示矩阵的转置
  //                          |0 -1  0|
  // E = U Sigma V'   let W = |1  0  0|
  //                          |0  0  1|
  // 得到4个解 E = [R|t]
  // R1 = UWV' R2 = UW'V' t1 = U3 t2 = -U3
  DecomposeE(E21,R1,R2,t);
  cv::Mat t1 = t;
  cv::Mat t2 = -t;

/**
 * @brief 分解Essential矩阵得到R,t
 * 分解E矩阵将得到4组解，这4组解分别为[R1,t],[R1,-t],[R2,t],[R2,-t]
 * 参考：Multiple View Geometry in Computer Vision - Result 9.19 p259
 * @param[in] E                 本质矩阵
 * @param[in & out] R1          旋转矩阵1
 * @param[in & out] R2          旋转矩阵2
 * @param[in & out] t           平移向量，另外一个取相反数
 */
void Initializer::DecomposeE(const cv::Mat &E, cv::Mat &R1, cv::Mat &R2, cv::Mat &t)
{
  // 准备存储对本质矩阵进行奇异值分解的结果
  cv::Mat u,w,vt;
  // 对本质矩阵进行奇异值分解
  cv::SVD::compute(E,w,u,vt);

  // 左奇异值矩阵U的最后一列就是t，对其进行归一化
  u.col(2).copyTo(t);
  t=t/cv::norm(t);

  // 构造一个绕Z轴旋转pi/2的旋转矩阵W，按照下式组合得到旋转矩阵 R1 = u*W*vt
  // 计算完成后要检查一下旋转矩阵行列式的数值，使其满足行列式为1的约束
  cv::Mat W(3,3,CV_32F,cv::Scalar(0));
  W.at<float>(0,1)=-1;
  W.at<float>(1,0)=1;
  W.at<float>(2,2)=1;

  // 计算
  R1 = u*W*vt;
  // 旋转矩阵有行列式为+1的约束，所以如果算出来为负值，需要取反
  if(cv::determinant(R1)<0)
    R1=-R1;

  // 同理将矩阵W取转置来按照相同的公式计算旋转矩阵R2 = u*W.t()*vt
  R2 = u*W.t()*vt;
  //旋转矩阵有行列式为1的约束
  if(cv::determinant(R2)<0)
    R2=-R2;
}