迁移学习（PCL）《PCL: Proxy-based Contrastive Learning for Domain Generalization》

论文信息

论文标题：PCL: Proxy-based Contrastive Learning for Domain Generalization
论文作者：
论文来源：
论文地址：download 
论文代码：download
引用次数：

1 前言

　　域泛化是指从一组不同的源域中训练一个模型，可以直接推广到不可见的目标域的问题。一个很有前途的解决方案是对比学习，它试图通过利用来自不同领域的样本到样本对之间丰富的语义关系来学习领域不变表示。一种简单的方法是将来自不同域的正样本对拉得更近，同时将其他负样本对推得更远。

　　在本文中，我们发现直接应用基于对比的方法（如有监督的对比学习）在领域泛化中是无效的。本文认为，由于不同域之间的显著分布差距，对准正样本到样本对往往会阻碍模型的泛化。为了解决这个问题，提出了一种新的基于代理的对比学习方法，它用代理到样本关系代替了原始的样本-样本关系，显著缓解了正对齐问题。

2 方法

　　整体框架

　　　　

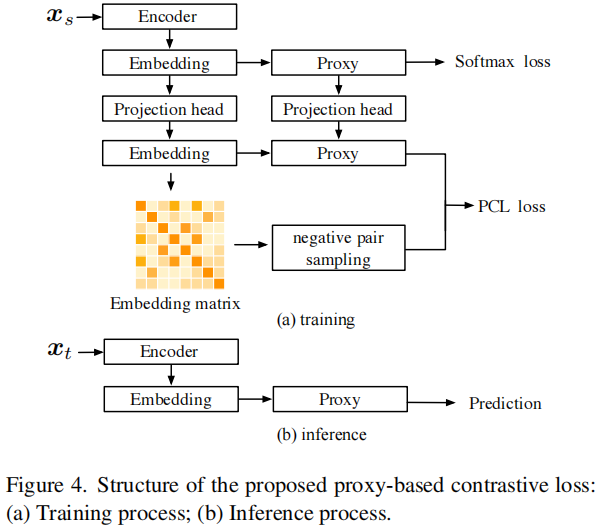
2.1 启发

　　现有对比学习的对比损失大多考虑正对和负对，本文受到 [ 61 ] 损失函数的启发，它只考虑正样本之间的关系，假设 $x_i$、$x_j$ 是从同一类的不同源域进行采样。设 $z=F_{\theta}(\boldsymbol{x})$ 是由特征提取器 $F_{\theta}$ 提取的特征，我们有： 

　　　　$\mathcal{L}_{\mathrm{pos}}=\frac{1}{\alpha} \log \left(1+\sum \exp \left(-\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{j} \cdot \alpha\right)\right)  \quad\quad\quad(1)$

　　实验：是否使用 包含正对之间对比的 $\text{instance} - \text{instance}$ 之间的对比学习？

　　　　

　　结果：单纯使用交叉熵损失比 交叉熵损失 +  正对之间的对齐 效果还好，所以跨域之间的正对对齐是有害的。

2.2 问题定义

　　多源域适应；

　　特征提取器：$F_{\theta}: X \rightarrow Z$

　　分类器：$G_{\psi}: \mathcal{Z} \rightarrow \mathbb{R}^{C}$

2.3 交叉熵回顾

　　交叉熵损失函数：

　　　　$\mathcal{L}_{\mathrm{CE}}=-\log \frac{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i}\right)}{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i}\right)+\sum_{j=1}^{C-1} \exp \left(\boldsymbol{w}_{j}^{\top} \boldsymbol{z}_{i}\right)}  \quad\quad\quad(2)$

　　其中，$\boldsymbol{w}_{c}$ 代表目标域的某一类中心；

　　$\text{Softmax CE}$ 损失只考虑了代理到样本的关系，而忽略了丰富的语义样本与样本之间的关系。

2.4 对比损失回顾

　　对比损失函数：

　　　　$\mathcal{L}_{\mathrm{CL}}=-\log \frac{\exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{+} \cdot \alpha\right)}{\exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{+} \cdot \alpha\right)+\sum \exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{-} \cdot \alpha\right)}$

　　基于对比的损失考虑了丰富的样本与样本之间的关系。其关键思想是学习一个距离，将 $\text{positive pairs}$ 拉近，将 $\text{negative pairs}$ 推远。

2.5 困难样本挖掘

　　公式：

　　　　$\begin{aligned}\mathcal{L}_{\mathrm{CL}} & =\lim _{\alpha \rightarrow \infty} \frac{1}{\alpha}-\log \left(\frac{\exp \left(\alpha \cdot s_{p}\right)}{\exp \left(\alpha \cdot s_{p}\right)+\sum_{j=1}^{N-1} \exp \left(\alpha \cdot s_{n}^{j}\right)}\right) \\& =\lim _{\alpha \rightarrow \infty} \frac{1}{\alpha} \log \left(1+\sum_{j=1}^{N-1} \exp \left(\alpha\left(s_{n}^{j}-s_{p}\right)\right)\right) \\& =\max \left[s_{n}^{j}-s_{p}\right]_{+} .\end{aligned}$

　　理解：由于域之间的域差异很大，简单的拉近正对之间的距离，拉远负对之间的距离是不合适的，这是由于往往存在某些难学的样本，使得模型总是识别错误。

2.6 基于代理的对比学习

　　$\text{Softmax}$ 损失 在学习类代理方面是有效的，能够快速、安全地收敛，但不考虑样本与样本之间的关系。基于对比损失利用了丰富的 样本-样本 关系，但在优化密集的 样本-样本 关系方面训练复杂性高。

　　　　$\mathcal{L}_{\mathrm{PCL}}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i} \cdot \alpha\right)}{Z}$

　　基于代理的对比损失：

　　　　$\mathcal{L}_{\mathrm{PCL}}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i} \cdot \alpha\right)}{Z}$

　　其中，

　　　　$Z=\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i} \cdot \alpha\right)+\sum_{k=1}^{C-1} \exp \left(\boldsymbol{w}_{k}^{\top} \boldsymbol{z}_{j} \cdot \alpha\right)+\sum_{j=1, j \neq i}^{K} \exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{j} \cdot \alpha\right)$

　　Note：$N$ 代表的是 $\text{batch_size}$ 的大小，$K$ 代表的是 $x_i$ 负样本的数量。

2.7 施加投影头的基于代理的对比学习

　　公式：

　　　　$\mathcal{L}_{\mathrm{PCL}-\mathrm{in}}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\boldsymbol{v}_{c}^{\top} \boldsymbol{e}_{i}\right)}{E}$

　　其中，

　　　　$E=\exp \left(\boldsymbol{v}_{c}^{\top} \boldsymbol{e}_{i}\right)+\sum_{k=1}^{C-1} \exp \left(\boldsymbol{v}_{k}^{\top} \boldsymbol{e}_{j}\right)+\sum_{j=1, j \neq i}^{B} \exp \left(\boldsymbol{e}_{i}^{\top} \boldsymbol{e}_{j}\right)$

2.8 训练

　　训练目标：

　　　　$\mathcal{L}_{\text {final }}=\mathcal{L}_{\mathrm{CE}}+\lambda \cdot \mathcal{L}_{\text {PCL-in }}$

3 实验结果

正对齐实验的细节

　　

消融实验

　　

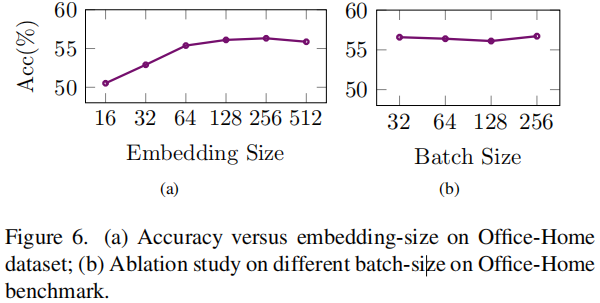
超参数实验

　　

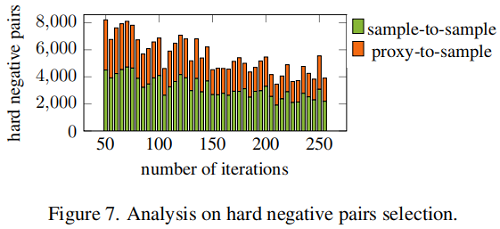
困难样本分析

　　

 

4 总结

　　略