全渠道定价、库存决策，混合整数规划建模求解，MNL选择模型，内附代码！
敲敲敲详细的高分牛刊论文阅读笔记，还有Python的PyLogit包详解！全渠道、运筹规划领域入门/基础模型，可提供写作灵感，内附论文的主要内容翻译解读、模型讲解和代码实现！
0. 写在前面
??刊论文！模型简单，代码实现更简单，墙裂推荐！可为运筹建模提供参考，也可作为全渠道零售研究的入门资料ε?(?> ? <)?з 全文有点长，前面先放一个博文结构和涉及内容：
-
第一部分为文章信息，主要介绍了这篇论文的基本信息、发表时间、研究方向，以及对论文难度的评价。
-
第二部分为主要内容，介绍了论文内容，帮助读者快速了解论文。
-
第三部分为模型构建，对文章中所涉及的模型进行了详细解释。
-
第四部分为代码求解，介绍了文章的求解方法，同时附加了Python的PyLogit库的详解，以及我尝试用PyLogit包去求解论文中MNL模型的代码。
1. 文章信息
-
基本信息
（1）发表期刊：Transportation Research Part E（10.047/Q1，运输领域的good good刊 ? ′? ? `? ??）
（2）标题：Fulfillment and pricing optimization for omni-channel retailers considering shipment of in-store demand（为考虑店内需求发货的全渠道零售商提供履行和定价优化）
（3）作者/发表时间：Khosro Pichka, Layth C. Alwan*, Xiaohang Yue / November 2022
（4）研究方向：运筹学，全渠道物流，定价，库存，MNL，混合整数规划
-
难度评价
（1）模型难度：★★★☆☆
（2）编程难度：★☆☆☆☆
（3）评价：适合用于入门全渠道物流/运筹调度，模型较为基础，但又因为它很基础，所以能给读者带来很多灵感和启发。这篇文章乍一看很难，甚至附录部分还将正文运筹模型的约束条件化为了80多条。但文中的非线性运筹模型，最后实际上化为了线性规划模型，作者直接用了Cplex求解；其他需要编程的部分，作者甚至直接import了python的包去解决 ?? ˙О˙??
2. 主要内容
2.1 摘要、关键字（翻译版）
摘要： 全渠道零售商通过电子商务渠道和不同区域的实体商店满足各地客户的需求。他们不仅可以通过电子履行中心来满足他们的线上订单，还可以通过实体店的店内库存来满足线上订单。另一方面，零售商可以使用定价决策来控制线上、实体渠道的需求。我们首先通过多项式 logit(MNL)选择模型，对客户需求进行建模。然后，我们提出了两个混合整数非线性规划（MINLP）模型，通过考虑履行和定价决策来最大化总利润。我们假设，如果商店库存不足，电子履行中心的库存也可以用作店内订单的备用库存，但仅适用于同一区域中的商店。我们还假设初始库存有限，并且在有限的销售范围内没有补货。在第二个 MINLP 模型中，我们还允许多种运输选项和库存决策。通过数值实验，我们表明全渠道零售商可以通过控制初始库存分配并通过电子履行库存满足店内需求来增加利润。
关键字：全渠道零售；跨渠道履行；定价；整数规划编程
2.2 研究思路
-
全渠道履行方式
请结合下图一起食用：
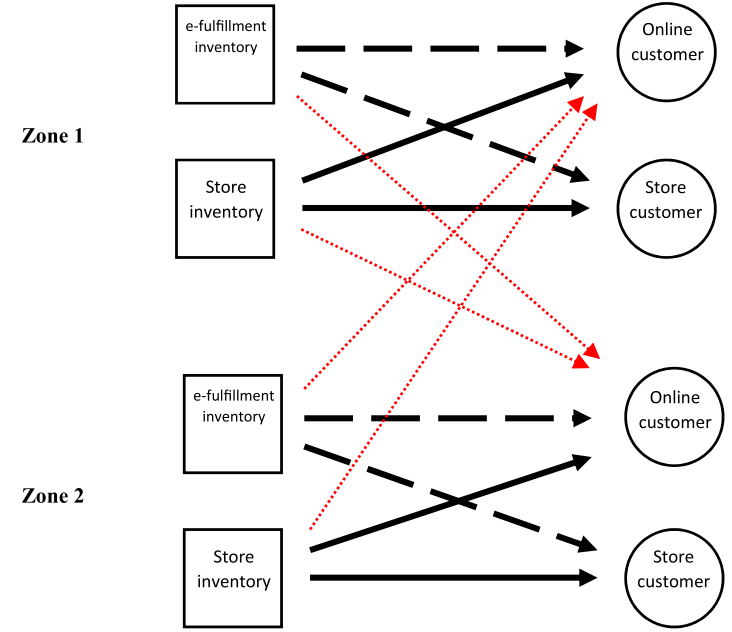
（1）每个区域都有各自的电子履行库存和门店库存，每个区域都有各自的实体店及实体店顾客，及通过线上渠道购买商品的线上顾客。
（2）对于同一地区，电子履行库存可满足该地区线上顾客的需求，门店库存可满足该地区实体店顾客的需求。当出现缺货情况时，电子履行库存和门店库存可互补，但履行成本会发生变化。
（3）对于不同地区，当电子履行库存发生缺货时，可使用另一地区的电子履行库存满足线上顾客的需求。对于实体店顾客的需求，不能通过跨区域调度电子履行库存来满足；对于门店库存，不能跨区域调度以满足其他区域的线上或线下顾客需求。
-
文章的研究思路
（1）利用多项式logit(MNL)选择模型，对客户需求进行建模，从而预估需求量。
（2）在得到客户需求量的基础上，第一个模型以最大化总利润为目标，考虑履行和定价决策。由于对库存是短期计划，故该模型不考虑库存持有成本。
（3）第二个模型在上一个模型的基础上进行拓展，对于库存，加入对库存持有成本的考虑；对于线上渠道履行方式，为客户增加常规运输和次日达的配送选项。模型在增加上述因素后，仍以最大化总利润为目标，考虑履行及定价决策。
（4）文章最后通过数值实验，表明全渠道零售商可以通过控制初始库存分配并通过电子履行库存满足店内需求来增加利润。
3. 模型建立
3.1 MNL选择模型的建立
文中MNL选择模型的建立，主要参考了Ben-Akiva等人1985年时发的一篇有关Travel Demand研究的论文，该篇论文链接如下：
Discrete Choice Analysis: Theory and Application to Travel Demand | SpringerLink
文中构建MNL选择模型的目的是预估线上、线下渠道的客户需求，以便后面建立运筹学模型。下面是文章建立MNL选择模型的过程：
-
假设客户效用的随机分量\(\xi_i\)是相互独立的，且服从\(Gumbel\)分布，累积分布函数为：
\[F(x)=P(\xi_i\leq x)=e^{-\mu(x-\eta)} \]其中，\(x\)是误差随机变量，\(\eta\)是位置参数，\(\mu\)是正比例函数。
随机变量\(\xi_i\)的均值和方差为：
\[E[\xi_i]=\eta+\frac{\gamma}{\mu}Var[\xi_i]=\frac{\pi^2}{6\mu^2} \]其中，\(\pi\approx3.14\)，\(\gamma\approx0.57\)(欧拉常数)
-
假设全渠道网络中共有\(Z\)个地区，客户从实体渠道购买的效用为\(U_{bz}\)，从网上渠道购买商品的效用为\(U_{ez}\)（对于\(z\)地区来说，\(z\in{Z}\)）
\[U_{bz}=u_{bz}+\xi_{bz} \]\[U_{ez}=u_{ez}+\xi_{ez} \]其中，\(u_{iz}(i\in{\{b,e\}})\)是选择\(i\)的效益，\(\xi_{iz}(i\in{\{b,e\}})\)是一个\(i.i.d. Gumber\)随机变量，所有的\(i\)均值为0，标度函数为1.
如果客户不从这些渠道购买，那么此时的平均效用为0，在这个效用模型下，客户选择渠道\(i\)购买的效益为：
\[\theta=\frac{e^{u_{iz}}}{\sum\limits_{j\in{\{e,b\}}}(e^{u_{jz}})+e^{u_0}}\forall{i}\in{\{e,b\}},\forall{z}\in{Z} \]其中，\(\theta_{iz}\)是客户从区域\(z\)中选择渠道\(i\)购买的概率，而\(u_0\)是客户选择不购买时的平均效用。
3.2 模型1的建立（短期规划）
-
假设选择\(i\)的平均效用\(u_{iz}(i\in{\{e,b\}})\)是一个关于渠道价格的线性函数。
\[u_{bz}=\beta_{0z}+\beta_{1z}P_{bz} \]\[u_{ez}=\beta_{0z}+\beta_{1z}P_{ez} \]其中，\(\beta_{0z}\)是常量，\(\beta_{1z}\)是在线或实体渠道中的价格系数，它可以通过使用历史数据计算。\(P_{iz}(i\in{{e,b}})\)是z区域的渠道为顾客提供的价格，它是一个向量。
价格向量函数\(P^t_z\)的计算方法如下：
\[D^t_{bz}(P^t_z)=n^t_z×\theta_{bz}D^t_{bz}(P^t_z)=n^t_z×\frac{e^{\beta_{0z}+\beta_{1z}P_{bz}}}{e^{\beta_{0z}+\beta_{1z}P_{bz}}+e^{\beta_{0z}+\beta_{1z}P_{ez}+1}} \]\[D^t_{ez}(P^t_z)=n^t_z×\theta_{ez}D^t_{ez}(P^t_z)=n^t_z×\frac{e^{\beta_{0z}+\beta_{1z}P_{bz}}}{e^{\beta_{0z}+\beta_{1z}P_{ez}}+e^{\beta_{0z}+\beta_{1z}P_{ez}+1}} \]其中，\(n^t_z\)是\(z\)区域\(t\)时间段的市场规模，\(\theta_{bz}\)、\(\theta_{ez}\)分别是客户从线下、线上渠道购买的概率。\(P^t_z=(P^t_{bz},P^t_{ez})\)是价格矢量，其包括在\(z\)区域\(t\)时间中提供的线下和线上渠道价格。
3.2.1 基本假设和符号说明
-
论文的基本假设如下：
（1）假设客户从线下渠道取货的平均效用与线上渠道相同。
（2）线下和线上渠道库存有限。
（3）销售周期有限，且分为T个周期。
（4）在周期t开始时，零售商公开每个销售区域z中的价格向量\(P^t_z=(P^t_{bz},P^t_{ez})\)，消费者可以据此了解到各个渠道的价格。
（5）线下和在线渠道在区域z中的需求表示为\(D^t_{bz}(P^t_z)\)和\(D^t_{ez}(P^t_z)\)
（6）不考虑补货和缺货，不考虑缺货成本。
-
论文的符号说明如下：
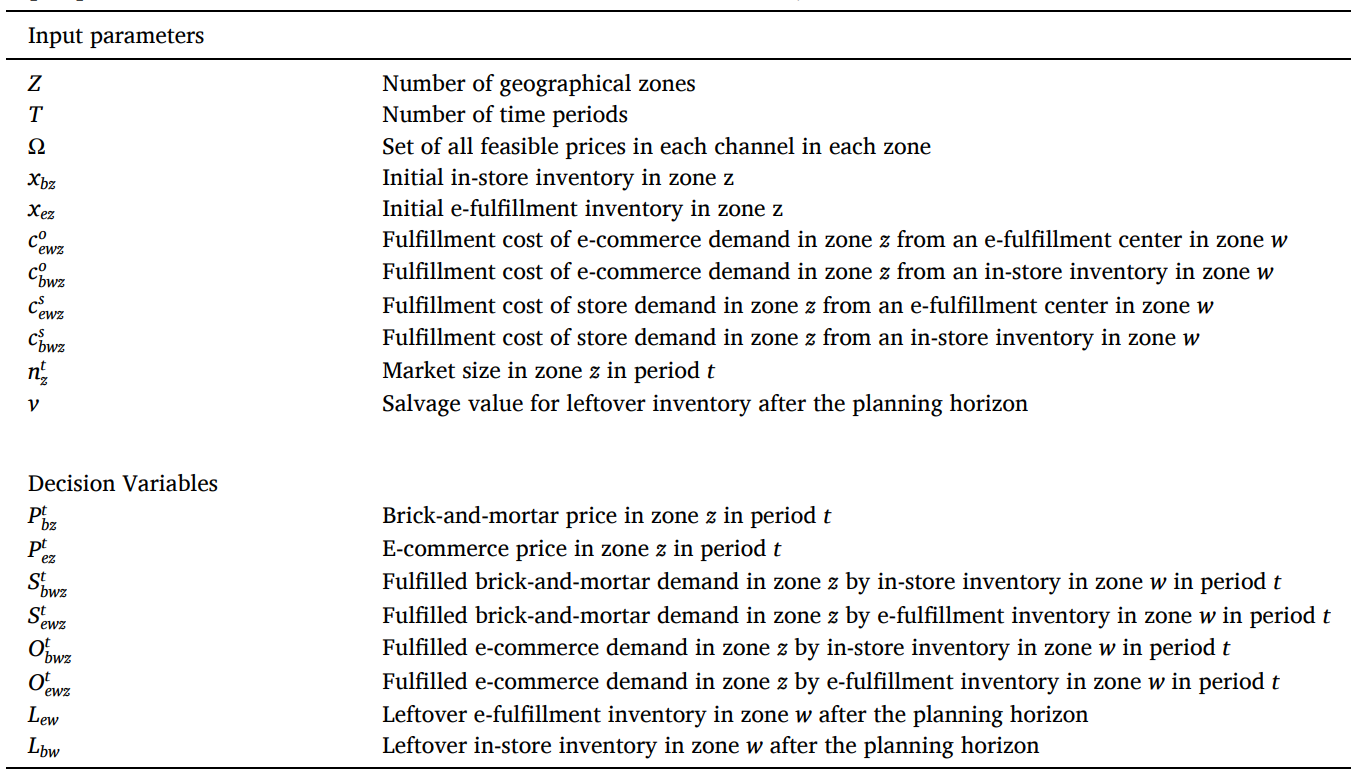
- 决策变量：\(S^t_{bwz}、S^t_{ewz}、O^t_{bwz}、O^t_{ewz}、L_{bz}、L_{ez}、P^t_{bz}、P^t_{ez}\)
3.2.2 模型建立
\(s.t.\)
-
目标函数为总利润最大化，主要分为三部分：第一部分为满足线上、线下渠道需求的收入；第二部分为剩余库存的价值；第三部分为线下、线上渠道的履行成本。
-
关于约束条件：第一、第二条约束条件为需求约束，即销售额必须小于对应渠道的需求；第三、第四条为剩余库存的计算；第五条为价格向量约束；其他约束条件为变量的非负约束。
3.3 模型2的建立（长期规划）
-
假设客户购买渠道为线下和线上渠道，其中线上渠道又可以选择常规运输和次日达两种配送方式。客户从商店购买产品的效用与网上购买到店取货（BOPS）的平均效用相同。基于此定义的客户效用函数为：
\[u_{bz}=\beta_{0z}+\beta_{1z}P_{bz}+\beta_{2z}t_{bz}+\beta_{3z}t_{bz}P_{bz} \]\[u_{fz}=\beta_{0z}+\beta_{1z}P_{fz}+\beta_{2z}t_{fz}+\beta_{3z}t_{fz}P_{fz} \]\[u_{sz}=\beta_{0z}+\beta_{1z}P_{sz}+\beta_{2z}t_{sz}+\beta_{3z}t_{sz}P_{sz} \]其中，\(P_{iz}\)、\(t_{iz}\)，\(i\in{\{b,f,s\}}\)分别代表向客户交付的价格、时间；\(b、f、s\)分别代表实体渠道、常规运输、次日达；\(\beta_{0z}\)是截距；\(\beta_{1z}\)分别是实体渠道、常规运输、次日达的价格系数；\(\beta_{2z}\)是交货时间系数；\(\beta_{3z}\)是价格与交货时间的相互作用系数。
-
假设有\(T\)个周期，在区域\(z\)，\(t\)时间段的市场规模为\(n^t_t\)。此时，线上和实体渠道对于区域\(z\)和时间\(t\)下不同的商品配送方式选择的需求函数遵循以下形式：
\[D^t_{bz}(P^t_z)=n^t_z×\frac{e^{u_{bz}}}{e^{u_{bz}}+e^{u_{fz}}+e^{u_{sz}}+1} \]\[D^t_{fz}(P^t_z)=n^t_z×\frac{e^{u_{fz}}}{e^{u_{bz}}+e^{u_{fz}}+e^{u_{sz}}+1} \]\[D^t_{sz}(P^t_z)=n^t_z×\frac{e^{u_{sz}}}{e^{u_{bz}}+e^{u_{fz}}+e^{u_{sz}}+1} \]其中，\(P^t_z\)为价格向量函数，\(P^t_z=(P^t_{bz},P^t_{fz},P^t_{sz})\)是价格矢量，在区域\(z\)时间段\(t\)中为线上和实体渠道提供的价格。
3.3.1 基本假设和符号说明
-
论文的基本假设如下：
（1）在周期\(t\)开始时，零售商在每个区域\(z\in{Z}\)设置价格向量\(P^t_z=(P^t_{bz},P^t_{fz},P^t_{sz})\)，确定价格后，估算实体渠道的需求\(D^t_{bz}(P^t_z), D^t_{fz}(P^t_z), D^t_{sz}(P^t_z)\)。
（2）假设零售商在每个区域都有一家商店和一个电子履行中心。
（3）不考虑缺货成本。
（4）店内库存可用于满足常规配送和次日达需求。
-
论文的符号说明如下：
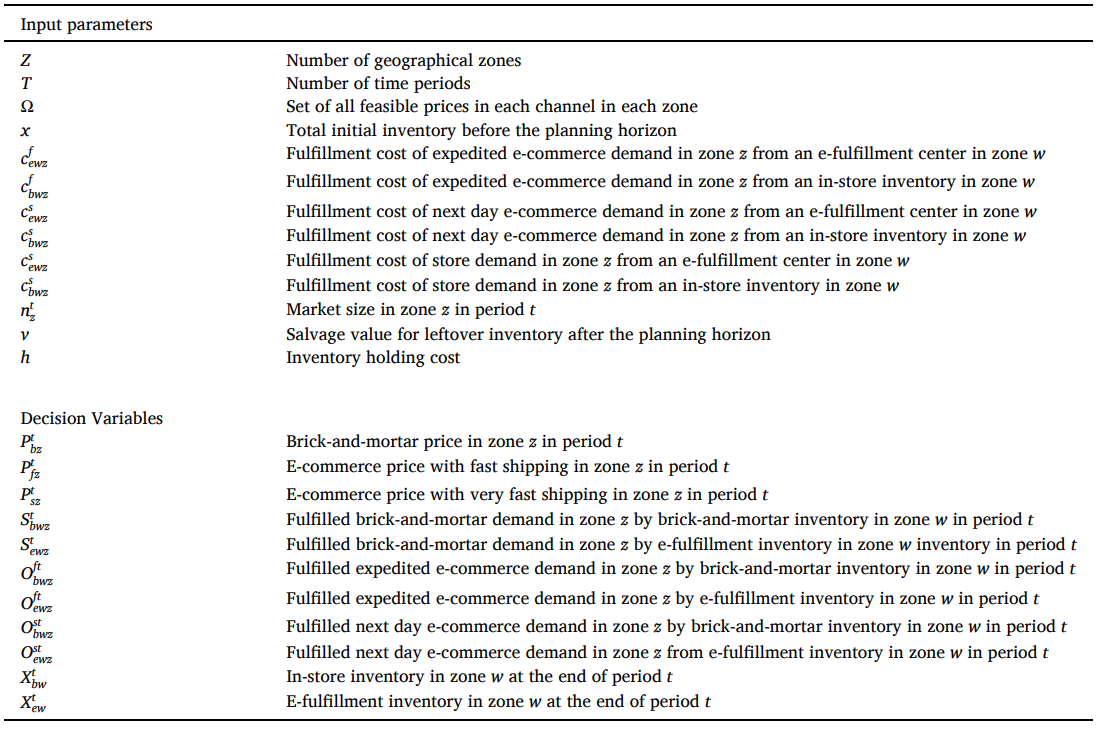
- 决策变量：\(S^t_{bwz}、S^t_{ewz}、O^{ft}_{bwz}、O^{ft}_{ewz}、O^{st}_{bwz}、O^{st}_{ewz}、P^t_{bz}、P^t_{fz}、P^t_{sz}、X_{bz}、X_{ez}\)
3.3.2 模型建立
\(s.t.\)
-
目标函数为总利润最大化，主要分为四部分：第一部分为满足线上、线下渠道需求的收入；第二部分为剩余库存的价值；第三部分为库存持有成本；第四部分为线下、线上渠道的履行成本。
-
关于约束条件：第一、第二、第三条约束条件为需求约束，即销售额必须小于对应渠道的需求；第四、第五条为区域\(z\)在\(t\)期末的剩余库存计算；第五条为库存约束，确保期初线上、线下的库存之和为整个计划期前的库存量；第六条为价格向量约束；其他约束条件为变量的非负约束。
4. 模型求解
文中的模型主要是用PyLogit和CPLEX求解器求解的，CPLEX求解比较简单，所以在这里不加赘述。但我发现有关PyLogit函数的资料居然全网都搜不到(╯‵□′)╯︵┻━┻，于是我采用了一些技术手段，找ChatGPT帮我写了个详解和代码。下面主要介绍PyLogit的详解及文章的MNL选择模型代码。
4.1 Python的PyLogit包详解
以下为ChatGPT的回答。
使用Python的PyLogit包求解MNL模型有以下几个步骤：
1. 计算变量并生成数据集
首先，您需要确定MNL模型中需要考虑哪些变量并将这些变量收集到一个数据集中。然后需要计算其中变量的值，这些值可能来自不同的数据集，可以直接从代码中读取，也可以从文件中读取到数据集中。在将数据集导入Python环境中之后，可以使用Pandas DataFrame属性计算变量。
2. 模型拟合
使用PyLogit包的模型拟合函数，您可以拟合MNL模型。这个函数将需要以下参数：
-
formula：一个字符串表示模型公式，语法可以参照R语言的glam()函数。
-
data：包含数据集和变量的Pandas DataFrame对象。
-
alt_name：一个字符串，是数据集中包含选择项的列名。
-
obs_id：一个字符串，表示数据集中包含观测编号的列名。
-
num_params：一个整数，表示模型参数的数量。
3. 模型评价
使用PyLogit包的模型评价函数评价模型。这个函数将需要以下参数：
-
model_results：包含模型拟合结果的PyLogit Mnlogit结果对象。
-
print_results：一个布尔值，表示是否打印出结果。
通过这些步骤完成之后，您将拟合一个MNL模型并可以使用PyLogit包进行相关的分析，如预测新数据等。
代码示例：
# 导入PyLogit包
from pylogit import PyLogit
# 从文件中读取数据集
data = pd.read_csv("data.csv")
# 计算变量
# ...
# 将变量添加到数据集中
# ...
# 指定模型公式
formula = 'Y ~ X1 + X2 + X3'
# 拟合模型
mnl_model = PyLogit(data=data,
formula=formula,
alt_name='Y',
obs_id='Obs_ID',
# num_params 等于 X1 + X2 + X3 中变量数量
num_params=3)
# 评估模型
mnl_model.fit(maxiter=1000, # 最大迭代次数
halton_iterations=0,
check_gradient=True)
# 打印结果
print(mnl_model.summary())
4.2 PyLogit求解MNL选择模型
我后面又询（奴）问（役）了一下ChatGPT，让它帮我写使用PyLogit包求解MNL选择模型的代码，以下代码是我根据GPT的代码进行修改，对论文中MNL选择模型的复现。
import numpy as np
import pandas as pd
import pylogit as pl
#ID代表客户的ID
#Choice代表客户对渠道的选择(b为线下渠道，e为线上渠道)
#Price代表对应的价格
data = pd.DataFrame({
'ID': [1, 1, 2, 2, 3, 3, 4, 4],
'Choice': ['b', 'e', 'b', 'e', 'b', 'e', 'b', 'e'],
'Price': [10, 8, 12, 6, 20, 15, 18, 10]
})
#'gev'是对Gumbel分布的定义
data['b_Price_Utility'] = pl.create_choice_column(data['Price'], 0.0, 'gev', (1,))
data['e_Price_Utility'] = pl.create_choice_column(data['Price'], 0.0, 'gev', (1,))
# 将数据重构为"wide"格式
long_data = pl.convert_wide_to_long(data, id_col='ID', alt_col='Choice',
observation_col=None, drop_alt_id=False)
wide_data = pl.convert_long_to_wide_format(long_data, id_col='ID',
value_col='Price Utility')
#使用MNL训练模型
model = pl.create_choice_model(data=wide_data, alt_id_col='alt_id',
obs_id_col='obs_id', choice_col='choice',
specification={
'Price': [1, 2]
},
model_type='MNL')
result = model.fit()
#输出模型的参数，里面包含了文中所需的β参数
print(result.summary())
代码中ID、Choice、Price的数据都是我乱编的，因为论文中没给训练数据集。但大家如果有需要的话可以自己收集数据读入训练。