存储论——经济订货批量的R实现
存储论又称库存理论,是运筹学中发展较早的分支。早在 1915 年,哈李斯(F.Harris)针对银行货币的储备问题进行了详细的研究,建立了一个确定性的存贮费用模型,并求得了最佳批量公式。1934 年威尔逊(R.H.Wilson)重新得出了这个公式,后来人们称这个公式为经济订购批量公式(简称为 EOQ 公式)。这是属于存贮论的早期工作。存贮论真正作为一门理论发展起来还是在二十世纪 50 年代的事。1958 年威汀 (T.M.Whitin)发表了《存贮管理的理论》一书,随后阿罗(K.J.Arrow) 等发表了《存贮和生产的数学理论研究》,毛恩(P.A.Moran)在 1959 年写了《存贮理论》。此后,存贮论成了运筹学中的一个独立的分支,有关学者相继对随机或非平稳需求的存贮模型进行了广泛深入的研究。
一、存储论概述
现代经济活动的生产和经营活动都离不开存储,为了使生产和经营活动有条不紊地进行,都需要一定数量的储备物资来支持。所谓存贮实质上是将供应与需求两个环节以存储中心联结起来,起到协调与缓和供需之间矛盾的作用。存储模型的基本形式如下图所示:
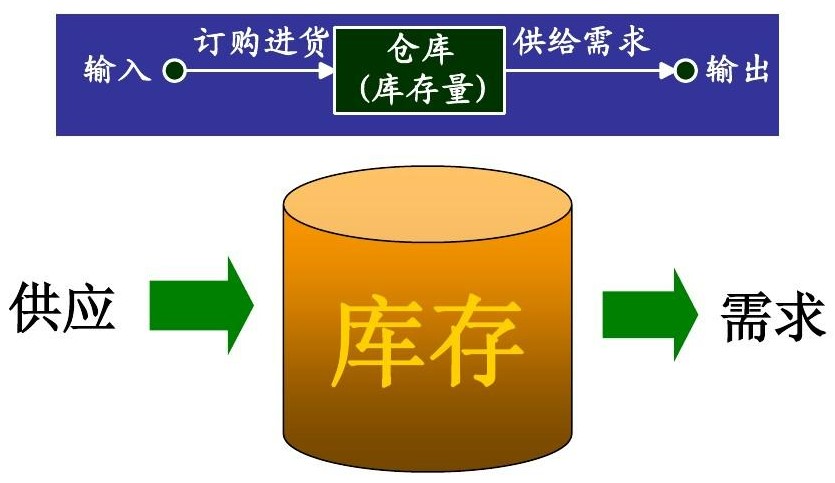
1.1 库存管理的基本要素
(1)需求率:单位时间内对某种物品的需求量,用 D 表示。
(2)订货批量:一次订货中,包含某种货物的数量,用Q 表示。
(3)订货间隔期:两次订货之间的时间间隔,用 T 表示。
1.2 库存管理的基本费用
(1)购置费:购置物品时花费的费用,即因购置物品而支出的货款,等于物品的单价乘以需求量。由于供应商一般会给一次订购某一数量的商品折扣价格,因此购置费可能会随着每次订购商品批量不同而改变。
(2)订货费\(C_1\)。指为补充而需要订购物品时支付的费用。其构成有两类,一是与订货次数有关的费用,如准备订单、洽商等。二是与订货次数无关的费用,如运费,办公管理等费用。
(3)存储费\(C_3\)。指为保存物品而支付的费用,如利息、折旧、损耗、财产税、保险等。现代管理把库存占用资金的机会成本(即这些资金若投资于他处所能获得的收益)也计入保管费中,而机会成本占保管费的比例在40%以上。保管费用可占到库存价值的20%~35%。保管费用往往用占库存价值的百分比来估算。
(4)缺货费\(C_2\)。由于存储不能满足需求而造成的损失。为补充订货往往比正常订货要增加额外的开支,为补足短缺造成加班加点的额外支出,未按期交货引起客户索赔、撤消合同甚至丧失市场等经济损失。
1.3 库存管理策略
所谓一个管理策略,是指决定什么情况下对存贮进行补充,以及补充数量的多少。 下面是一些比较常见的库存管理策略。
(1)t 循环策略:不论实际的存贮状态如何,总是每隔一个固定的时间t ,补充 一个固定的存储量Q 。
(2)(t,S) 策略:每隔一个固定的时间 t 补充一次,补充数量以补足一个固定的最大存储量 S 为准。因此,每次补充的数量是不固定的,要视实际存储量而定。当存储(余额)为 I 时,补充数量为Q = S ? I 。
(3)(s,S) 策略:当存储(余额)为 I ,若 I > s ,则不对存储进行补充;若 I ≤ s , 则对存储进行补充,补充数量Q = S ? I 。补充后达到最大存储量 S。s 称为订货点(或 保险存贮量、安全存贮量、警戒点等)。
在很多情况下,实际存储量需要通过盘点才能 得知。若每隔一个固定的时间t 盘点一次,得知当时存储 I ,然后根据 I 是否超过订货点 s,决定是否订货、订货多少,这样的策略称为(t,s,S)策略。
二、确定性存储模型
存储论的数学模型一般分成两类:一类是确定性模型,它不包含任何随机因素,另一类是带有随机因素的随机存贮模型,这里主要总结确定性存储模型。
2.1 经典的EOQ订货模型
| 模型1 | 模型2 | 模型3 | 模型4 | |
|---|---|---|---|---|
| 模型假设 | 需求是连续的、均匀的,需求速度是常数 R(单位时间的需求量);补充可以瞬间实现,补充时间 t 近似为 0;单位 C1 存储费不变;每次订货量 Q 不变,订购费 C3 不变,货物单价 K 不变;单位缺货成本 C2 为无穷大 | 在模型1假设基础上,补货需要一定时间,不考虑拖延时间,只考虑生产(装配)时间,生产速度是连续均匀的周期的,生产速度为常数 P(P>R);单位存储费为 C1,单位缺货费 C2,单位订购费为 C3 | 与模型二相比,不容许缺货!!!,补货时间较长 | 与模型二相比,补货时间极短,容许缺货 |
| 模型状态图 | 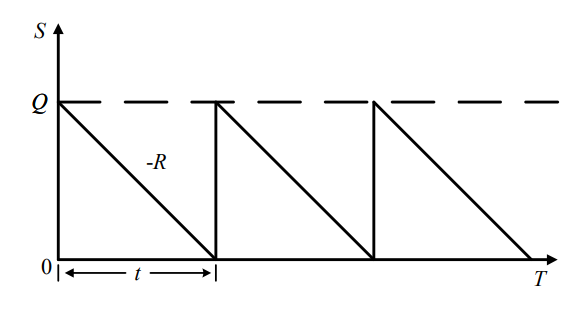 |
 |
 |
 |
| 单位时间的总平均费用 | \(C(t)=\frac{C_3}{t}+KR+\frac{1}{2}C_1Rt\) | \(C(t)=\frac{1}{t}[\frac{1}{2}C_1(P-R)\frac{Rt^2}{P}+C_3]\) | \(C(t, S)=\frac{1}{t}[\frac{C_1S^2}{2R}+\frac{C_2(Rt-S)^2}{2R}+C_3]\) | \(C(t, t_2)=\frac{1}{2}\frac{(P-R)R}{P}[C_1 t-2 C_1 t_2+(C_1+C_2) \frac{t_2^2}{t}]+\frac{C_3}{t}\) |
| 最佳定货周期 | \(t^*=\sqrt{\frac{2 C_3}{C_1 R}}\) | \(t^*=\sqrt{\frac{2 C_3}{C_1 R}}\cdot \sqrt{\frac{P}{P-R}}\) | \(t^*=\sqrt{\frac{2 C_3}{C_1 R}}\cdot \sqrt{\frac{C_2}{C_1+C_2}}\) | \(t^*=\sqrt{\frac{2 C_3}{C_1 R}} \cdot \sqrt{\frac{C_1+C_2}{C_2}} \cdot \sqrt{\frac{P}{P-R}}\) |
| 最大缺货量 | 0 | 0 | $$B^* = \sqrt{\frac{2 C_1 C_3 R}{C_2(C_1+C_2)}} $$ | \(B^*=\sqrt{\frac{2 C_1 C_3 R}{\left(C_1+C_2\right) C_2}} \cdot \sqrt{\frac{P-R}{P}}\) |
| 最佳定货量 | \(Q^*=R t^*=\sqrt{\frac{2 C_3 R}{C_1}}\) | \(Q^*=\sqrt{\frac{2 C_3 R}{C_1}}\cdot \sqrt{\frac{P-R}{P}}\) | \(Q^*=\sqrt{\frac{2 C_3 R}{C_1}} \cdot \sqrt{\frac{C_1+C_2}{C_2}}\) | \(Q^*=\sqrt{\frac{2 C_3 R}{C_1}} \cdot \sqrt{\frac{C_1+C_2}{C_2}} \cdot \sqrt{\frac{P}{P-R}}\) |
| 最大存储量 | \(Q^*=\sqrt{\frac{2 C_3 R}{C_1}}\) | $ S^* = \sqrt{\frac{2 C_3 R}{C_1}} \cdot \sqrt{\frac{P-R}{P}} $ | \(S^*=\sqrt{\frac{2 C_3 R}{C_1}} \cdot \sqrt{\frac{C_2}{C_1+C_2}}\) | \(S^*=\sqrt{\frac{2 C_3 R}{C_1}} \cdot \sqrt{\frac{C_2}{C_1+C_2}} \cdot \sqrt{\frac{P-R}{P}}\) |
| 最小费用 | $C^*=\sqrt{2 C_1 C_3 R} $ | $C^*=\sqrt{2 C_1 C_3 R}\cdot \sqrt{\frac{P}{P-R}} $ | $C^*=\sqrt{2 C_1 C_3 R}\cdot \sqrt{\frac{C_2}{C_1+C_2}} $ | \(C^*=\sqrt{2 C_1 C_3 R} \cdot \sqrt{\frac{C_2}{C_1+C_2}} \cdot \sqrt{\frac{P-R}{P}}\) |
2.2 经济订购批量的折扣模型
经济订购批量折扣模型是经济订购批量存贮模型的一种发展,即商品的价格 是不固定的,是随着订货量的多少而改变的。就一半情况而论,物品订购的越多,物品的单价也就越低,因此折扣模型就是讨论这种情况下物品的订购数量。 一年花费的总费用由三个方面组成:年平均存贮费、年平均订货费和商品的购买费用,即
比如说订购量为 \(Q\), 其单价 \(K(Q)\) :
对应的平均单位货物所需费用为:
对 \(C^1(Q)\) 求得极值点为 \(Q_0\), 若 \(Q_{j-1} \leq Q_0<Q_j\), 求
设从此式得到的最小值为 \(C^l\left(Q_{l-1}\right)\), 则取 \(Q^*=Q_{l-1}\) 。
三、存储策略的R计算
经济订货批量 economic order quantity (EOQ),通过平衡采购进货成本和保管仓储成本核算,以实现总库存成本最低的最佳订货量。经济订货批量是固定订货批量模型的一种,可以用来确定企业一次订货(外购或自制)的数量。当企业按照经济订货批量来订货时,可实现订货成本和储存成本之和最小化。
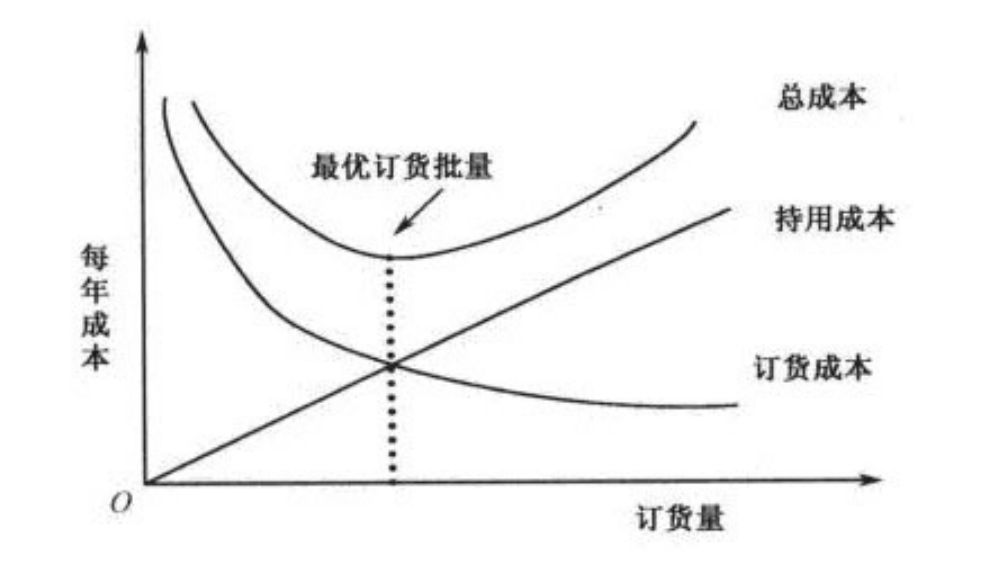
经济订货批量 economic order quantity (EOQ),通过平衡采购进货成本和保管仓储成本核算,以实现总库存成本最低的最佳订货量。经济订货批量是固定订货批量模型的一种,可以用来确定企业一次订货(外购或自制)的数量。当企业按照经济订货批量来订货时,可实现订货成本和储存成本之和最小化。
总结
存储系统可以用“供-存-销”三个活动来描述,通过订货以及货后的存储与销售来满足顾客的需求,或者说由于生产或销售的需求,从存储系统中取出一定量的库存货物,这就是存储系统的输出。存储的货物由于不断的输出而减少,必须及时的补充,补充就是存储系统的输入,补充可以通过外部订货,采购等活动来进行,也可以通过内部的生产活动来进行,在这个系统中,决策者可以通过控制订货时间的间隔和订货量的多少来调节系统的运行,使得在某种准则下系统运行达到最优因此,存储论中研究的主要问题可以概括为,何时订货(补充存贮),每次订多少货(补充多少库存)这两个问题。
