蒙特卡罗方法:当丢失确定性时的处理办法
一、简介
蒙特卡罗(Monte Carlo),也可翻译为蒙特卡洛,只是不同的音译选词,比较常用的是蒙特卡罗。是摩洛哥的一片城区,以拥有豪华赌场闻名,蒙特卡罗方法是基于概率的。基本思想:如果你想预测一件事情的结果,你只要把随机生成的各种输入值,把这件事模拟很多遍,根据模拟出的结果就可以看到事情的结果大致是什么情况。蒙特卡罗算法是基于蒙特卡罗方法的算法。
二、应用
1. 计算π
在白纸中间画一个正方形,在正方形里画一个内切的圆。假设正方形的边长为a,正方形面积S正=a2,圆的半径为a/2,圆的面积S圆=π(a/2)2。则S圆/S正=π/4,即圆的面积是正方形面积的π/4倍,接下来我们通过数值模拟来计算这两个面积。
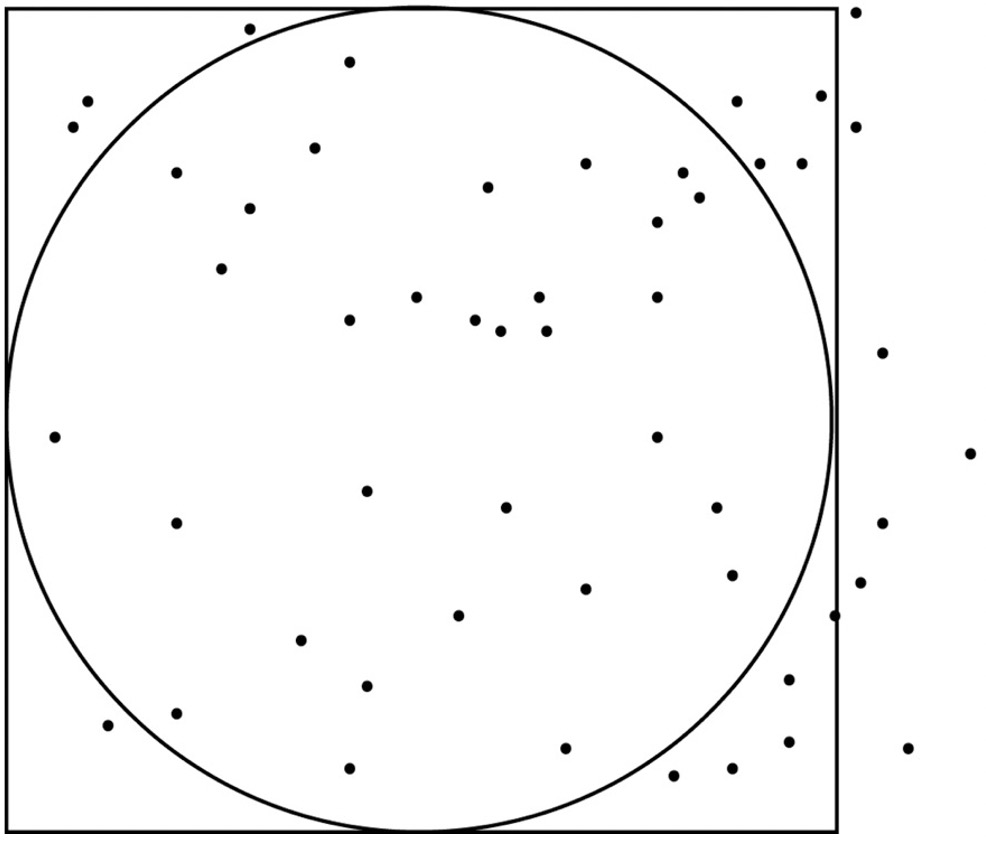
你找些小颗粒,比如小米或者花粉之类的,随机洒落在白纸上。白纸上有了足够多的颗粒之后,你数一数落在正方形里的小颗粒有多少个——这个数字代表正方形的面积;再数一数落在圆形里的小颗粒有多少个——这个数字代表圆的面积。那么这代表小颗粒数量的两个数字之比,就应该约等于圆形和正方形的面积之比即π/4。你只需要数一数就可以计算出π大约等于几。通过大量均匀洒落小颗粒可以让π值更精确,显然这个方法不够精确——但是这个方法却很有用。很多时候我们根本无法对方程精确求解,那么蒙特卡罗方法就是你的朋友。
2. 原子弹的研制
在第二次世界大战中,美国原子弹的研制就第一次用到了蒙特卡罗方法。原子弹的爆炸依赖于裂变时产生的链式反应反应。在链式反应中,核物质中游离的中子会撞击铀原子,释放大量的能量,同时释放出来三个新的中子。这些中子如果又能撞击其它铀原子,链式反应就会发生。这样原子弹就能爆炸了。但释放出来的中子是不是能撞击到其它铀原子,是一个不确定的过程。这些中子运动的方向,携带的能量是随机的。如果整个核物质的质量太小,很有可能中子被释放出来之后,直接离开了核物质,没撞击到任何铀原子,那链式反应就不会发生,原子弹就爆炸不了了。在核物理中有一个概念,叫“临界质量”,是让链式反应能够发生的最小质量。而这个临界质量,就是对各个中子运动中的随机变量进行取样,通过蒙特卡罗模拟算法计算得到。
三、注意事项
1. 蒙特卡罗方法是对问题的估算,而不是精确计算。
2. 蒙特卡罗方法的成功,非常依赖于参数和模型的正确。
比如我是北京国安的狂热球迷,认为国安打哪只球队的胜率都是90%。结果其他球队这一年都引入了特厉害的外援,实力大增。不对这些信息进行考虑,修正国安90%的胜率,那随机模拟的结果就是不可信的。模拟次数再多,也没用。
最近大火的AI如Chat-GPT有资料显示使用了蒙特卡罗方法。GPT-3的参数有1750亿个,根据OpenAI的CEO山姆·阿尔特曼(Sam Altman)说GPT-4的参数并不比GPT-3多很多,但大家猜测,GPT-5的参数将会是GPT-3的100倍。
3. 蒙特卡罗方法会减小我们发现问题本质的机会。
我们知道GPT很厉害,可是不知道GPT为什么厉害。
四、启示
蒙特卡罗方法在哲学上是一种随机试验,在物理学上是通过人为制造的随机性——噪声来探索系统的多个可能性,在数学上,它还有一个惊喜:能减少计算量!也许是因为有了噪声自动代表了多种可能性,有了噪声,你不用太高的分辨率和预测精度就能达到很不错的计算结果。
