信息论之从熵、惊奇到交叉熵、KL散度和互信息
一、熵(PRML)
考虑将A地观测的一个随机变量x,编码后传输到B地。
这个随机变量有8种可能的状态,每个状态都是等可能的。为了把x的值传给接收者,需要传输?个3?特的消息。注意,这个变量的熵由下式给出:
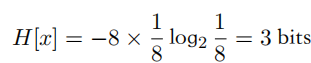
?均匀分布?均匀分布的熵要?。
如果概率分布非均匀,同样使用等长编码,那么并不是最优的。相反,可以根据随机变量服从的概率分布构建Huffman树,得到最优的前缀编码。
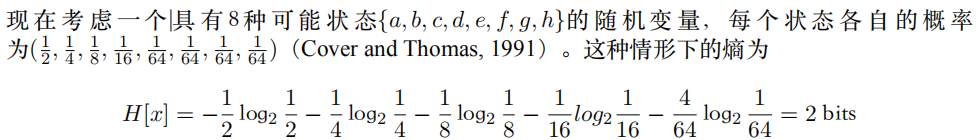
可以利??均匀分布这个特点,使?更短的编码来描述更可能的事件,使?更长的编码来描述不太可能的事件。
可以使?下?的编码串:0、10、110、1110、111100、111101、111110、111111来表?状态{a, b, c, d, e, f, g, h}。传输的编码的平均长度就是
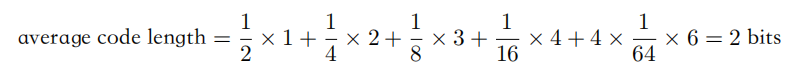
?噪声编码定理(noiseless coding theorem)表明,熵是传输?个随机变量状态值所需的?特位的下界。
事实上,熵的概念最早起源于物理学,是在热?学平衡的背景中介绍的。后来,熵成为描述统计?学中的?序程度的度量。
考虑?个集合,包含N个完全相同的物体,这些物体要被分到若?个箱?中,使得第i个箱?中有ni个物体。考虑把物体分配到箱?中的不同?案的数量。有N种?式选择第?个物体,有(N -1)种?式选择第?个物体,以此类推。
因此总共有N!种?式把N个物体分配到箱?中,其中N!表?乘积N × (N -1) × · · · × 2 × 1。然?,我们不想区分每个箱?内部物体的重新排列。在第i个箱?中,有ni!种?式对物体重新排序,因此把N个物体分配到箱?中的总?案数量为:
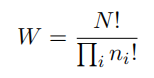
这被称为乘数(multiplicity)。熵被定义为通过适当的参数放缩后的对数乘数,即
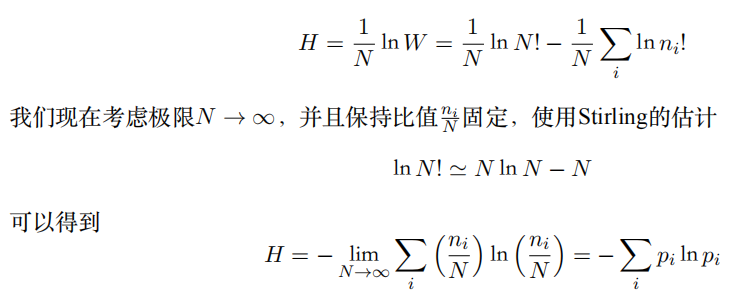
二、惊奇与信息
考虑关于?个随机试验中可能出现的事件E。当我们真正观察到事件E时,我们接收到了多少信息呢?对事件E的惊奇程度取决于E发生概率,越是不可能的事件发生,带来的惊奇程度越大

- 如果有?告诉我们?个相当不可能的事件发?了,我们收到的信息要多于我们被告知某个很可能发?的事件发?时收到的信息。
- 如果听到?个必然事情,那么就不会接收到信息。EX: 明天有24h
对惊奇程度进行量化:信息量可看成E发生时的“惊讶程度”(消除不确定性的程度)
对于信息内容的度量将依赖于概率分布p(x),因此想要寻找?个函数h(x),它是概率p(x)的单调递增函数,表达了信息的内容。
h(·)的形式可以这样寻找:
- 如果有两个不相关的事件x和y,那么观察到两个事件同时发?时获得的信息应该等于观察到事件各?发?时获得的信息之和,即h(x, y) = h(x) + h(y)。
- 两个不相关事件是统计独?的,因此p(x, y) = p(x)p(y)。
根据这两个关系,很容易看出h(x)?定与p(x)的对数有关。因此有:h(x) = -log2p(x)。
- 其中,负号确保了信息?定是正数或者是零。
- 注意,低概率事件x对应于?的信息量。
- 对数的底遵循信息论使?2作为对数的底(2进制编码最短)。
h(x)的单位是?特(bit, binary digit)。

随机变量的熵,衡量了其分布下的编码长度(概率值的倒数的对数)的期望,即平均编码长度。

三、熵的相关变量
熵用于衡量不确定性,其相当于是编码一个随机变量的平均最小编码长度(最优编码的下界,即huffman编码)
1.自信息-二进制编码长度
\[\frac{1}{q(x)}
\]
2.信息熵
\[ H\Big(p(x)\Big)
= - \int p(x)\ln p(x)dx
\\ = \int p(x)\ln \frac{1}{p(x)}dx
= \mathbb{E}_{x\sim p(x)}\left[\ln\frac{1}{p(x)}\right]
\]
3.交叉熵,用一个分布p(x)的编码去编码另一个分布q(x)的代价(平均编码长度)
\[C\Big(p(x)\Big\Vert q(x)\Big)
= - \int p(x)\ln q(x)dx
\\ = \mathbb{E}_{x\sim p(x)}\left[\ln\frac{1}{q(x)}\right]
\]
分布q(x)的自信息(最小编码长度)关于分布p(x)的期望
Ex: q(x1) = 0.25需要2bits,例如00来编码,但p(x1)=0.01
,相当于用更短的编码来编码低频取值(不符合高频短码),可能导致编码代价更大。
随机变量取值越多,熵越大(信息增益)
4.KL散度,衡量两个分布p(x)和q(x)的距离(不相似程度):
用一个分布p(x)的编码去编码另一个分布q(x)的额外代价
若KL散度为0,则表示编码额外代价为0,即两个分布相同
\[ KL\Big(p(x)\Big\Vert q(x)\Big)
= - \int p(x)\ln \frac{q(x)}{p(x)} dx
= \int p(x)\ln \frac{p(x)}{q(x)} dx
\\= \int p(x)\ln p(x) - p(x)\ln q(x)dx
\\ = - \int p(x)\ln q(x)dx - (-\int p(x)\ln p(x) )
\\ = C\Big(p(x)\Big\Vert q(x)\Big) - H\Big(p(x)\Big)
\\ =
\mathbb{E}_{x\sim p(x)}\left[\ln\frac{p(x)}{q(x)}\right] \]
由于熵为常数项,最小化交叉熵,相当于最小化KL散度(最大似然),离散形式即求和。
- 互信息

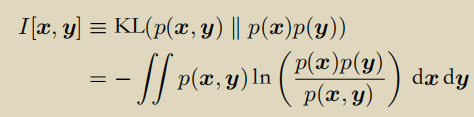
联合分布p(x, y)和边缘分布乘积累p(x)p(y)的KL散度。
如果互信息为0,则两个边缘分布独立p(x, y) = p(x) p(y)
