论文解读（PAWS）《Semi-Supervised Learning of Visual Features by Non-Parametrically Predicting View Assignments with Support Samples》

论文信息

论文标题：Semi-Supervised Learning of Visual Features by Non-Parametrically Predicting View Assignments with Support Samples
论文作者：Mahmoud Assran, Mathilde Caron, Ishan Misra, Piotr Bojanowski, Armand Joulin, Nicolas Ballas
论文来源：NeurIPS 2021
论文地址：download 
论文代码：download
视屏讲解：click

1 介绍

　　提出问题：充分利用无标注目标；

　　解决办法：对无标注数据使用一种可信的伪标签策略；

2 方法

2.1 整体框架

　　

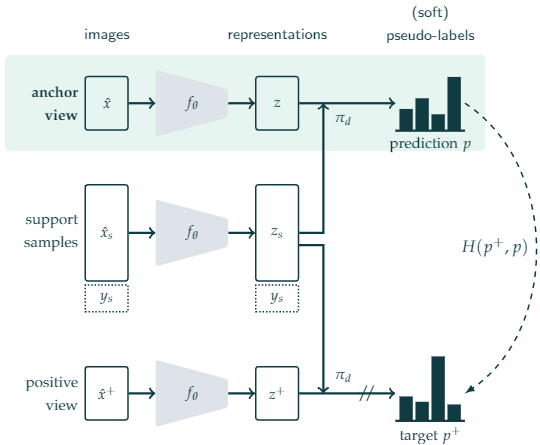
2.2 问题定义

　　We consider a large dataset of unlabeled images  $\mathcal{D}=   \left(\mathrm{x}_{i}\right)_{i \in[1, N]}$  and a small support dataset of annotated images  $\mathcal{S}=\left(\mathbf{x}_{s i}, y_{i}\right)_{i \in[1, M]}$ , with  $M \ll N  $.Our goal is to learn image representations by leveraging both  $\mathcal{D}$  and  $\mathcal{S}$  during pretraining. After pre-training with  $\mathcal{D}$  and  $\mathcal{S}$ , we fine-tune the learned representations using only the labeled set  $\mathcal{S}$ .

2.3 相似度分类器

　　公式：

　　　　$\pi_{d}\left(z_{i}, \mathbf{z}_{\mathcal{S}}\right)=\sum_{\left(z_{s_{j}}, y_{j}\right) \in \mathbf{z}_{\mathcal{S}}}\left(\frac{d\left(z_{i}, z_{s j}\right)}{\sum_{z_{s k} \in \mathbf{z}_{\mathcal{S}}} d\left(z_{i}, z_{s k}\right)}\right) y_{j}$

　　Note：Soft Nearest Neighbours strategy 

　　其中：

　　　　$d(a, b) =\exp \left( \frac{a^{T} b}{\|a\|\|b\| \tau} \right)$

　　简化：

　　　　$p_{i}:=\pi_{d}\left(z_{i}, \mathbf{z}_{\mathcal{S}}\right)=\sigma_{\tau}\left(z_{i} \mathbf{z}_{\mathcal{S}}^{\top}\right) \mathbf{y}_{\mathcal{S}}$

　　Note：$p_{i} \in[0,1]^{K}$

　　锐化：

　　　　$\left[\rho\left(p_{i}\right)\right]_{k}:=\frac{\left[p_{i}\right]_{k}^{1 / T}}{\sum_{j=1}^{K}\left[p_{i}\right]_{j}^{1 / T}}, \quad k=1, \ldots, K$

　　Note：锐化目标会鼓励网络产生自信的预测，避免模型崩溃问题。 

2.4 训练目标

　　总目标：

　　　　$\frac{1}{2 n} \sum_{i=1}^{n}\left(H\left(\rho\left(p_{i}^{+}\right), p_{i}\right)+H\left(\rho\left(p_{i}\right), p_{i}^{+}\right)\right)-H(\bar{p})$

　　ME-MAX 正则化项：$H(\bar{p})$

　　其中：

　　　　$\bar{p}:=\frac{1}{2 n} \sum_{i=1}^{n}\left(\rho\left(p_{i}\right)+\right.   \left.\rho\left(p_{i}^{+}\right)\right) $ 表示所有未标记表示的锐化预测的平均值；

　　该正则化项在鼓励个体预测有信心的同时，鼓励平均预测接近均匀分布。ME-MAX 正则化项之前已在判别式无监督聚类社区中用于平衡学习的聚类大小[35]。

　　Note：交叉熵

# Example of target with class indices
loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()
# Example of target with class probabilities
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5).softmax(dim=1)
output = loss(input, target)
output.backward()

3 总结

　　略