【LeetCode动态规划#07】01背包问题一维写法(状态压缩)实战,其二(目标和、零一和)
目标和(放满背包的方法有几种)
难度:中等
给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
- 输入:nums: [1, 1, 1, 1, 1], S: 3
- 输出:5
解释:
- -1+1+1+1+1 = 3
- +1-1+1+1+1 = 3
- +1+1-1+1+1 = 3
- +1+1+1-1+1 = 3
- +1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
提示:
- 数组非空,且长度不会超过 20 。
- 初始的数组的和不会超过 1000 。
- 保证返回的最终结果能被 32 位整数存下。
思路
前者是将集合分成两个相等的子集,后者是将集合分成两个尽可能相等的子集
共同点是什么?都是先把问题转换成将当前题目给的数组集合一分为二
因此,本题要往01背包问题上靠,也要先转换为一个将集合划分成两部分的问题
怎么转呢?
题目要在一个非负整数数组nums中的任意一个整数前加正负号,实现所有元素相加后等于目标值target,最后统计一共有多少种相加的方法(即一共有多少种放正负号的方法)
那么我们就可以把数组元素分为两个子集,一个子集中的元素前面都加正号,另一个子集则都加负号
这不就有两个子集了嘛(md这正常人能想到?)
设加负号的子集为 negativeSign, 加正号的子集为 plusSign
注意,此时我们讨论的两个子集都是已经通过dp划分好的,里面不带正负号
那么,两个子集的元素相加应该等于非负整数数组nums的元素之和sum
两个子集的元素相减应该等于目标值target
抽象为公式如下:
① plusSign + negativeSign = sum;
② plusSign - negativeSign = target;
合并一下可以得到: plusSign = (sum + target) / 2;
在01背包问题中,只需用一个子集充当背包即可,因此这里可以选择 加正号的子集plusSign 作为背包
以示例 nums: [1, 1, 1, 1, 1], target: 3 来说
转换为背包问题后,背包的容量为 (5+3)/2 = 4 ,所谓的"物品"就是nums数组中的元素
当然,这里用除法就会涉及不能整除的情况
若不能整除,代表该数组nums找不到能够组合成目标值target的方法,直接return 0
此时,问题就转换成了:使用非负整数数组nums中的元素装满背包有几种方法?
(注意,本题要找的是有几种装满背包的方法)
区分一下之前做的背包问题的目标
? 单纯的01背包问题:装满某个背包时,物品的最大价值;
? 分割等和子集:往背包放入物品后,背包的最大重量(换句话说就是能不能用物品把背包装满,能就return true)
? 最后一块石头:往背包装物品,能装下的最大价值(能装多少装多少)
五步走
1、确定dp数组含义
老规矩,先回顾一下经典01背包问题的dp数组定义
dp[j]: 背包容量为j时,装满背包的最大价值为dp[j]
转换一下,本题的dp数组含义可以定义如下:使用所给的所有物品,装满容量为j的背包有dp[j]种方法
2、确定递推公式
怎么推导出dp[j]呢?
这里要通过"物品"的角度来想,例如,当前如果有一个物品(nums中的一个元素)要放入背包,假设背包容量是5(与示例保持一致, nums元素为5个1)
那么这个物品一定会放入背包中,因此也一定会占用掉背包的一部分容量,占用掉的容量是 j - nums[i]
根据dp数组的含义,在有一个物品确定放入的情况下,dp[5]就会转变为dp[5 - 1],也就是dp[4]
有点乱?那再用直接一点的话描述一下上面发生的事情:
? 1、最开始,背包容量是5,此时按dp数组的定义,装满该背包会有dp[5]种方法;(因为还有五个容量,你随便怎么装,所有的方法就表示为dp[5])
? 2、当已经有一个"物品"确定放入容量为5的背包时,背包容量缩减为4(不管你开始没开始往里面放,先给你预留了),还是按定义,此时装满该背包会有dp[5-nums[0]]种方法(即dp[5 - 1] = dp[4])
? 3、当已经有两个"物品"确定放入容量为5的背包时,背包容量缩减为3(不管你开始没开始往里面放,先给你预留了)
? 按定义,此时装满该背包会有dp[5-nums[0]-nums[1]]种方法(即dp[5-1-1] = dp[3])
后面的情况以此类推
注意,一定要结合dp数组的定义
这里的
dp[某某]指的是在"某某"容量下放入物品时,所有方法的集合
简单概括一下,例如:dp[j],j为5,
- 已经有0个的话,有 dp[5]种方法 凑成 容量为5的背包。
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]种方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]种方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]种方法 凑成 容量为5的背包
那凑整dp[5]有多少方法呢?(即dp[5]怎么求)
就把所有的 dp[j - nums[i]] 累加起来即可
也就是dp[5] = dp[4] + dp[3] + dp[2] + dp[1] + dp[0]
总结为递推公式就是:
dp[j] += dp[j - nums[i]]
该递推公式很重要,在用背包解决排列组合问题时还能用
3、初始化dp数组
一切结合dp数组的含义:装满容量为j的背包有dp[j]种方法
来看dp[0]的情况
dp[0]即被包容量为0时装满背包的方法数量,这里又可以细分为两种情况:要装的物品重量不为0和重量为0
如果物品重量不为0
那么实际上我们是无法将该物品装入容量为0的背包中的,那么是不是就意味着在该种情况下,dp[0] = 0 了呢?
我认为也不是,因为背包容量为0是一种特殊情况,此时不论你往不往里面放东西(或者放不放得进),背包都已经处于放满状态,因此
dp[0]应该是默认有一种方式装满的,那就是什么也不放
由上述分析可知,dp[0]应该初始化为1,即dp[0] = 1;
如果物品重量为0
接着上面的分析,若背包中物品重量为0, 假设:[0,0,0,0,0], target = 0
那这些0就还是可以往背包里面放的(放不放都一样),并且不同的物品(重量为0)往背包放就算是一种不同的放法
因此,dp[0]就是这五个重量为0的物品不断组合放入背包内的组合方式的种类数量
大概有32种,于是dp[0] = 32
以上分析是建立在认同dp[0]应该初始化为1的情况下成立的(因为其他情况都是基于的dp[0] = 1推导出来的)
说了这么多,无非就是像说明清楚dp[0]初始化为1的可行性,记住本题 dp[0] = 1 就行
4、确定遍历顺序
仍然遵循先遍历物品(nums),后遍历背包容量的顺序,且背包容量的遍历方向是倒序的
这里在逻辑上与之前涉及重量的问题不太一样,下面手动推导一遍
(输入:nums: [1, 1, 1, 1, 1], target: 3)
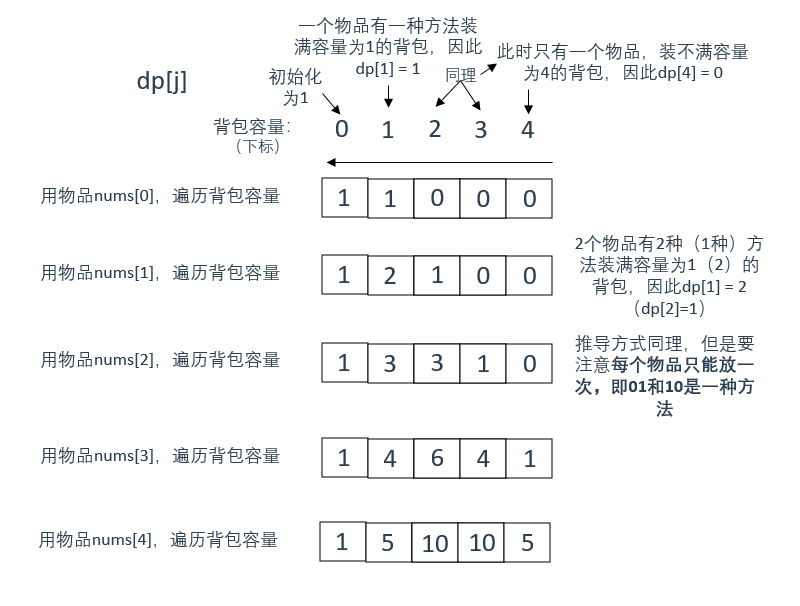
如图所示为遍历过程
注意dp数组的含义,使用所给的所有物品,装满容量为j的背包有dp[j]种方法
这里有两个关键点:1、需要使用所有的物品;2、装满
- 不论遍历的过程如何,最终我们需要求的是把所有物品放入容量为j的背包的方法,因为遍历物品的过程是一个一个遍历的,所以放入所有物品的方法种类也是由最开始的情况不断累加到最后才能得到的
- 一定要能够装满当前容量才算是一种方法,比如在容量为4的情况下,目前遍历到第一个物品(也就是只有一个物品),无论如何是放不满4个容量的,因此就算能够放入当前的一个物品,也不能算一种方法
说一下"装满方法"是怎样计算的
因为01背包问题中,每个物品只能使用一次,那么在当前物品能够装满当前容量的前提下,使用相同物品以不同顺序放入背包的方法应该视作同一种方法
什么意思呢?就是说假设现在遍历到了nums[2],我们手头上有3个物品,此时容量遍历到2的话,理论上我们有以下放入的方式:
nums[0] nums[1] nums[2]
nums[0] nums[2] nums[1]
nums[1] nums[0] nums[2]
nums[1] nums[2] nums[0]
nums[2] nums[1] nums[0]
nums[2] nums[0] nums[1]
其中,有一半的放入方式重复使用了物品,因此是不计入方法种类
代码
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
//计算数组元素之和
int sum = 0;
for(auto num : nums) sum += num;
//判断两种无解的情况
//1、所给的target已经大于sum
//2、(sum + target) / 2不能整除,即计算背包容量时不能整除
if(abs(target) > sum) return 0;//取绝对值
if((sum + target) % 2 != 0) return 0;
//计算背包容量
int bagSize = (sum + target) / 2;
//定义dp数组
vector<int> dp(bagSize + 1, 0);
//初始化dp数组
dp[0] = 1;
//遍历dp数组
for(int i = 0; i < nums.size(); ++i){//遍历物品num
// 如果当前背包容量小于物品重量,换一个物品继续遍历容量(所以第二层循环的条件是j >= nums[i])
// 每一个元素一定是不可重复放入,所以从大到小遍历
for(int j = bagSize; j >= nums[i]; --j){//遍历背包容量
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
零一和
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
- 输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
- 输出:4
- 解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
- 输入:strs = ["10", "0", "1"], m = 1, n = 1
- 输出:2
- 解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
- 1 <= strs.length <= 600
- 1 <= strs[i].length <= 100
- strs[i] 仅由 '0' 和 '1' 组成
- 1 <= m, n <= 100
思路
这题有点绕的其实,刚上手的话很容易将m、n看成两个容器
其实这样想是错误的,本题实质上还是01背包问题,只不过这个背包有"两个维度"
什么意思呢?我解释一下
先来说题意吧,题目要求是:m代表字符串中0的个数,n代表字符串中1的个数
然后,题目规定一组m、n,要求从字符串数组strs中找到能够满足m、n的最大子集,并返回该子集的大小
拿示例1来看,strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
最多有 5 个 0 和 3 个 1 的strs中的最大子集是 {"10(m=1,n=1)","0001(m=3,n=1)","1","0"}
该子集的大小是4,因此结果值返回的是4
看出来了吗?其实题目规定的"m = 5, n = 3"就是在设置背包的容量
确定了背包就好办了,下面就套五部曲解决问题
五步走
1、确定dp数组的含义
注意,这里题目是要求最大子集个数,也就是背包中物品的个数
那么dp数组可以定义如下
dp[i][j]: 在背包"容量"(这里的容量指的是strs中一个子字符串中0、1的个数)为i、j时能够装下物品的最大个数
虽然这里需要把dp数组设置成二维的,但其实本质上和之前的一维01背包问题没有区别
如果不好理解的话还是可以把dp数组看成是个一维的,例如dp[G],G是背包的容量,只不过G由两个部分组成,一部分是i,一部分是j
(这里也可以把G想象成strs中一个子字符串,例如"10")
2、确定递推公式
因为本题只是给放入背包的物品多增加了一个维度,所以递推公式可以参考标准01背包问题的递推公式(一维)
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
那么对照着本题的递推公式就是
dp[i][j] = max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1(物品数量));
解释一下,
当我们确定放入一个新的子字符串(假设是"10"),那么此时背包容量(i、j)就要对应减少子字符串中0的个数(zeroNums)、子字符串中1的个数(oneNums),(zeroNums, oneNums)即为该子字符串(物品)的重量
当然,此时包内的物品数量要加1(类比之前的递推公式,背包总价增加)
推导dp[i][j]时,有两种情况:放东西和不放东西
这两者取能够使物品个数最大的那种情况就行,即上面的递推公式
3、初始化dp数组
dp[0][0]时要初始化为0,即容量为(0,0)时,一个也装不下
然后其余的部分也要初始化为0,为了防止递推值被初始值覆盖(详见)
4、确定遍历顺序

和普通的01背包的一维解法一样,这里也是先遍历物品(子字符串),然后倒序遍历背包容量(i,j)(对应(zeroNums, oneNums))
核心代码如下,结合上面的图来解释
for (string str : strs) { // 遍历物品,即子字符串,例如"10"
int oneNum = 0, zeroNum = 0;
for (char c : str) {//统计字符串中0、1的数量
if (c == '0') zeroNum++;
else oneNum++;
}//以下是遍历背包容量(i,j)
//如果当前背包容量(i,j)小于物品重量(zeroNum,oneNum),换一个物品(子字符串)再放入
for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
对应到图中就是,我们第一轮遍历是从最下面的一行开始的,从右往左倒序遍历
根据递推公式有:dp[3][3] = max(dp[3][3], dp[3 - 1][3 - 1] + 1);(此时子字符串是"10")
因为dp[3][3]的初始值为0,所以dp[2][2]+1肯定要大一些,故dp[3][3] = dp[3 - 1][3 - 1] + 1;
那dp[2][2]又是多少?还是用递推公式去算,得到dp[2][2] = max(dp[2][2], dp[2 - 1][2 - 1] + 1);,取决于dp[1][1]
同理,dp[1][1] = max(dp[1][1], dp[1 - 1][1 - 1] + 1);,最后可以算出dp[1][1]=dp[0][0]+1=1
所以,
dp[2][2]=1+1=2
dp[3][3]=2+1=3
此时可以得到图中dp[3][3]处的递推值,同理可以把整个dp数组的递推值计算出来,结果如上图所示
代码
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
//定义dp数组,并初始化
//二维数组,行列分别是0、1(可以颠倒)
vector<vector<int>> dp(m + 1, vector(n + 1, 0));
//遍历dp数组
for(string str : strs){//遍历物品(子字符串)
int zeroNums = 0, oneNums = 0;
//统计字符串中的01个数
for(char c : str){
if(c == '0'){
zeroNums++;
}else oneNums++;
}
for(int i = m; i >= zeroNums; --i){//遍历背包容量(i,j),倒序
for(int j = n; j >= oneNums; --j){//i\j遍历顺序可以更换,因为本质上还是容量
dp[i][j] = max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1);
}
}
}
return dp[m][n];
}
};
