迁移学习（COAL）《Generalized Domain Adaptation with Covariate and Label Shift CO-ALignment》

论文信息

论文标题：Generalized Domain Adaptation with Covariate and Label Shift CO-ALignment
论文作者：Shuhan Tan, Xingchao Peng, Kate Saenko
论文来源：ICLR 2020
论文地址：download 
论文代码：download
视屏讲解：click

1 摘要

　　提出问题：标签偏移；

　　解决方法：

　　　　原型分类器模拟类特征分布，并使用 Minimax Entropy 实现条件特征对齐；

　　　　使用高置信度目标样本伪标签实现标签分布修正；

2 介绍

2.1 当前工作

　　假设条件标签分布不变 $p(y \mid x)=q(y \mid x)$，只有特征偏移 $p(x) \neq q(x)$，忽略标签偏移 $p(y) \neq q(y)$。

　　假设不成立的原因：

• • 场景不同，标签跨域转移 $p(y) \neq q(y)$ 很常见；
  • 如果存在标签偏移，则当前的 UDA 工作性能显著下降；
  • 一个合适的 UDA 方法应该能同时处理协变量偏移和标签偏移；

2.2 本文工作

　　本文提出类不平衡域适应 (CDA)，需要同时处理 条件特征转移 和 标签转移。

　　具体来说，除了协变量偏移假设 $p(x) \neq   q(x)$, $p(y \mid x)=q(y \mid x)$，进一步假设 $p(x \mid y) \neq q(x \mid y)$ 和 $p(y) \neq q(y)$。

　　CDA 的主要挑战：

• • 标签偏移阻碍了主流领域自适应方法的有效性，这些方法只能边缘对齐特征分布；
  • 在存在标签偏移的情况下，对齐条件特征分布 $p(x \mid y)$, $q(x \mid y)$ 很困难；
  • 当一个或两个域中的数据在不同类别中分布不均时，很难训练无偏分类器；

　　CDA 概述：

　　

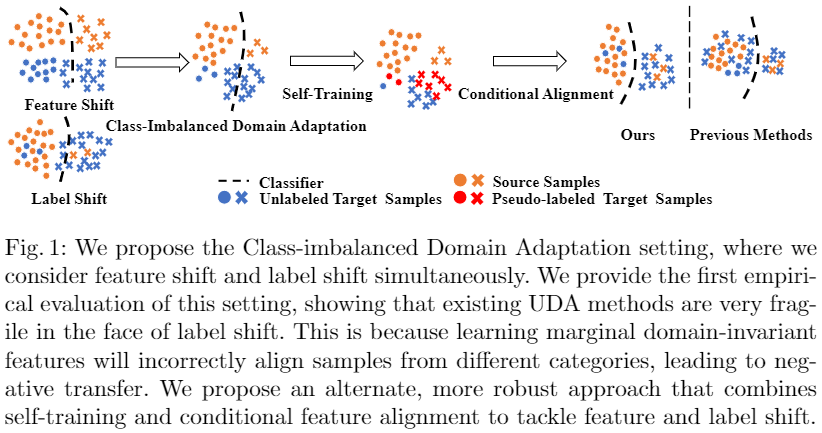
3 问题定义

　　In Class-imbalanced Domain Adaptation, we are given a source domain  $\mathcal{D}_{\mathcal{S}}=   \left\{\left(x_{i}^{s}, y_{i}^{s}\right)_{i=1}^{N_{s}}\right\}$  with  $N_{s}$  labeled examples, and a target domain  $\mathcal{D}_{\mathcal{T}}=\left\{\left(x_{i}^{t}\right)_{i=1}^{N_{t}}\right\}$  with  $N_{t}$  unlabeled examples. We assume that  $p(y \mid x)=q(y \mid x)$  but  $p(x \mid y) \neq   q(x \mid y)$, $p(x) \neq q(x)$ , and  $p(y) \neq q(y)$ . We aim to construct an end-to-end deep neural network which is able to transfer the knowledge learned from  $\mathcal{D}_{\mathcal{S}}$  to  $\mathcal{D}_{\mathcal{T}}$ , and train a classifier  $y=\theta(x)$  which can minimize task risk in target domain  $\epsilon_{T}(\theta)=\operatorname{Pr}_{(x, y) \sim q}[\theta(x) \neq y]$. 

4 方法

4.1 整体框架

　　

4.2 用于特征转移的基于原型的条件对齐

　　目的：对齐 $p(x \mid y)$ 和 $q(x \mid y)$

　　步骤：首先使用原型分类器（基于相似度）估计 $p(x \mid y)$ ，然后使用一种 $\text{minimax entropy}$ 算法将其和 $q(x \mid y)$ 对齐；

4.2.1 原型分类器

　　原因：基于原型的分类器在少样本学习设置中表现良好，因为在标签偏移的假设下中，某些类别的设置频率可能较低；

# 深层原型分类器
class Predictor_deep_latent(nn.Module):
    def __init__(self, in_dim = 1208, num_class = 2, temp = 0.05):
        super(Predictor_deep_latent, self).__init__()
        self.in_dim = in_dim
        self.hid_dim = 512
        self.num_class = num_class
        self.temp = temp  #0.05

        self.fc1 = nn.Linear(self.in_dim, self.hid_dim)
        self.fc2 = nn.Linear(self.hid_dim, num_class, bias=False)

    def forward(self, x, reverse=False, eta=0.1):
        x = self.fc1(x)
        if reverse:
            x = GradReverse.apply(x, eta)
        feat = F.normalize(x)
        logit = self.fc2(feat) / self.temp
        return feat, logit

　　源域上的样本使用交叉熵做监督训练：

　　　　$\mathcal{L}_{S C}=\mathbb{E}_{(x, y) \in \mathcal{D}_{S}} \mathcal{L}_{c e}(h(x), y)  \quad \quad \quad(1)$

　　样本 $x$ 被分类为 $i$ 类的置信度越高，$x$ 的嵌入越接近 $w_i$。因此，在优化上式时，通过将每个样本 $x$ 的嵌入更接近其在 $W$ 中的相应权重向量来减少类内变化。所以，可以将 $w_i$ 视为 $p$ 的代表性数据点（原型） $p(x \mid y=i)$ 。

4.2.2 通过 Minimax Entropy 实现条件对齐

　　目标域缺少数据标签，所以使用 $\text{Eq.1}$ 获得类原型是不可行的；

　　解决办法：

• • 将每个源原型移动到更接近其附近的目标样本；
  • 围绕这个移动的原型聚类目标样本；

　　因此，提出 熵极小极大 实现上述两个目标。

　　具体来说，对于输入网络的每个样本 $x^{t} \in \mathcal{D}_{\mathcal{T}}$，可以通过下式计算分类器输出的平均熵

　　　　$\mathcal{L}_{H}=\mathbb{E}_{x \in \mathcal{D}_{\mathcal{T}}} H(x)=-\mathbb{E}_{x \in \mathcal{D}_{\mathcal{T}}} \sum_{i=1}^{c} h_{i}(x) \log h_{i}(x)\quad \quad \quad(2)$

　　通过在对抗过程中对齐源原型和目标原型来实现条件特征分布对齐：

• • 训练 $C$ 以最大化 $\mathcal{L}_{H}$ ，旨在将原型从源样本移动到邻近的目标样本；
  • 训练 $F$ 来最小化 $\mathcal{L}_{H}$，目的是使目标样本的嵌入更接近它们附近的原型；

4.3 标签转移的类平衡自训练

　　由于源标签分布 $p(y)$ 与目标标签分布 $q(y)$ 不同，因此不能保证在 $\mathcal{D}_{\mathcal{S}}$ 上具有低风险的分类器 $C$ 在 $\mathcal{D}_{\mathcal{T}}$ 上具有低错误。 直观地说，如果分类器是用不平衡的源数据训练的，决策边界将由训练数据中最频繁的类别主导，导致分类器偏向源标签分布。 当分类器应用于具有不同标签分布的目标域时，其准确性会降低，因为它高度偏向源域。

　　为解决这个问题，本文使用[19]中的方法进行自我训练来估计目标标签分布并细化决策边界。自训练为了细化决策边界，本文建议通过自训练来估计目标标签分布。 我们根据分类器 $C$ 的输出将伪标签 $y$ 分配给所有目标样本。由于还对齐条件特征分布 $p(x \mid y$ 和 $q(x \mid y)$，假设分布高置信度伪标签 $q(y)$ 可以用作目标域的真实标签分布 $q(y)$ 的近似值。 在近似的目标标签分布下用这些伪标记的目标样本训练 $C$，能够减少标签偏移的负面影响。

　　为了获得高置信度的伪标签，对于每个类别，本文选择属于该类别的具有最高置信度分数的目标样本的前 $k%$。利用 $h(x)$ 中的最高概率作为分类器对样本 $x$ 的置信度。 具体来说，对于每个伪标记样本 $(x, y)$，如果 $h(x)$ 位于具有相同伪标签的所有目标样本的前 $k%$ 中，将其选择掩码设置为 $m = 1$，否则 $m = 0 $。将伪标记目标集表示为 $\hat{\mathcal{D}}_{T}=\left\{\left(x_{i}^{t}, \hat{y}_{i}^{t}, m_{i}\right)_{i=1}^{N_{t}}\right\}$，利用来自 $\hat{\mathcal{D}}_{T}$ 的输入和伪标签来训练分类器 $C$，旨在细化决策 与目标标签分布的边界。 分类的总损失函数为：

　　　　$\mathcal{L}_{S T}=\mathcal{L}_{S C}+\mathbb{E}_{(x, \hat{y}, m) \in \hat{\mathcal{D}}_{T}} \mathcal{L}_{c e}(h(x), \hat{y}) \cdot m$

　　通常，用 $k_{0}=5$ 初始化 $k$，并设置 $k_{\text {step }}=5$，$k_{\max }=30$。

　　Note：本文还对源域数据使用了平衡采样的方法，使得分类器不会偏向于某一类。

4.4 训练目标

　　总体目标：

　　　　$\begin{array}{l}\hat{C}=\underset{C}{\arg \min } \mathcal{L}_{S T}-\alpha \mathcal{L}_{H} \\\hat{F}=\underset{F}{\arg \min } \mathcal{L}_{S T}+\alpha \mathcal{L}_{H}\end{array}$

5 总结

　　略