所谓图(graph),是图论中基本的数学对象,包括一些顶点,和连接顶点的边。
图可以分为有向图和无向图,有向图中的边是有方向的,而无向图的边是双向连通的。

用一个二维数组来记录各个点之间的关系,若u到v之间有一条边则可用map[u][v]=1来表示,具体如下

对应的无向图为
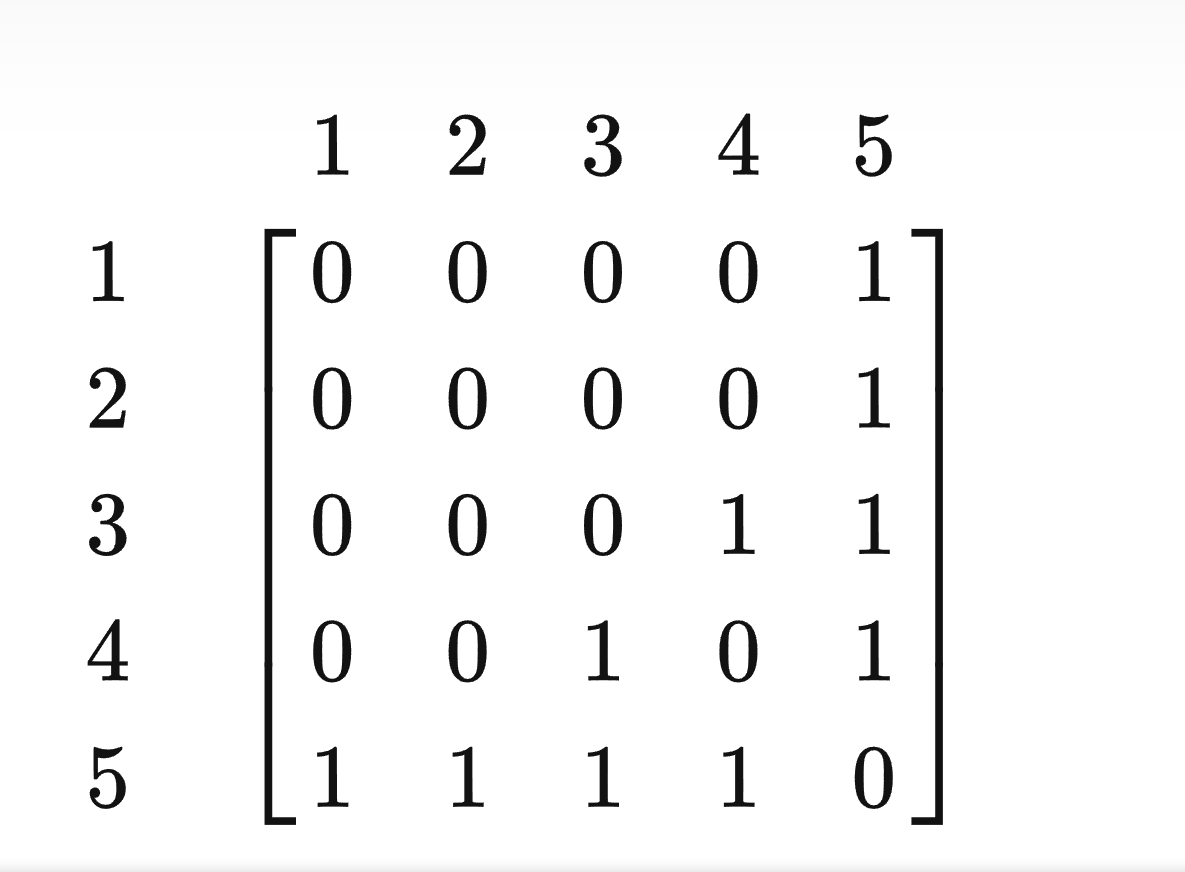
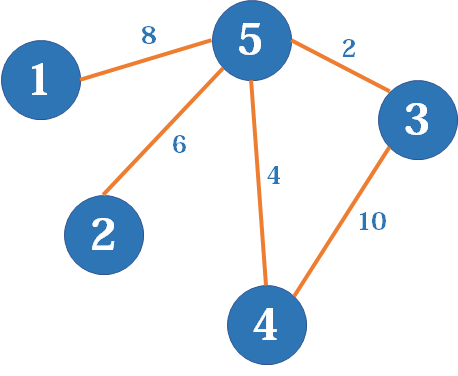
对于带权图 将1改成权值即可
邻接矩阵的优点显而易见:简单好写,查询速度快。但缺点也很明显:空间复杂度太高了。 n个点对应大小 n^2的数组,如果点的数量达到10000,这种方法就完全不可行了。
首先,我们用一个结构体vector存储每个边的起点和终点,然后用一个二维vector存储边的信息。
用map[a][b]=c 来表示顶点为a的第b条边是c号边
以下面为例:
8 9
1 2 //0号边
1 3 //1号边
1 4 //2号边
2 5 //3号边
2 6 //4号边
3 7 //5号边
4 7 //6号边
4 8 //7号边
7 8 //8号边
最终二维vector中存储的是如下信息
0 1 2 //1号顶点连着0、1、2号边
3 4 //2号顶点连着3、4号边
5 //3号顶点连着5号边
6 7 //4号顶点连着6、7号边
//5号顶点没有边
//6号顶点没有边
8 //7号顶点连着8号边
//8号顶点没有边
1 #include<iostream>
2 #include<algorithm>
3 #include<vector>
4 using namespace std;
5
6 struct edge {
7 int st, ed;
8 };
9 vector <int> map[100001];
10 vector <edge> vec;
11 int main() {
12
13 int n, m;
14 cin >> n >> m;
15 for (int i = 0; i < m; i++) {
16 int st, ed;
17 cin >> st >> ed;
18 vec.push_back({ st, ed }); //初始化存边的s数组
19 }
20
21 for (int i = 0; i < m; i++)
22 map[vec[i].st].push_back(i);
23 //初始化map数组,vec[i].st表示顶点,在该顶点加入其对应的边
24
25 return 0;
26 }
如何去遍历呢?
x表示顶点
map[x].size()表示该顶点具有边的个数
map[x][i]表示x顶点的第i条边是哪一条边
vec[map[x][i]].ed 表示x顶点的第i条边的边的终点
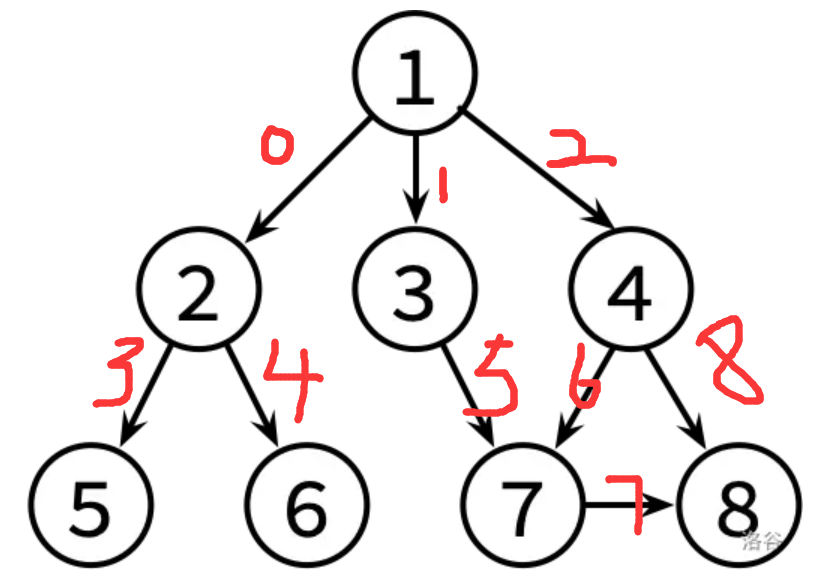
以该图为例:
map[1][0]表示 0 号边 map[2][0]表示第3条边 map[4[1]表示第8条边
那么vec[map[1][0]].st就等于2号顶点
1 void dfs(int x) {
2 cout << x<<" ";
3
4 for (int i = 0; i < map[x].size(); i++)
5 {
6 int j = vec[map[x][i]].ed;
7 if (!st[j])
8 {
9 st[j] = 1;
10 dfs(j);
11 }
12 }
13 }
idx是边的编号,a是边的起点,b是边的终点
e[idx] 存idx号边指向的点。
h[a] 存从a号点出发的某一条边的编号
ne[idx] 存idx号边(起点为a)的上一条边(也是以a为起点的)
i=ne[i]循环遍历所有从a出发的边
输出邻接表:
1:->4->7->2
2:->5->8->1
3:->9->4
4:->6->3->1
5:->2
6:->4
7:->1
8:->2
9:->3
对比原图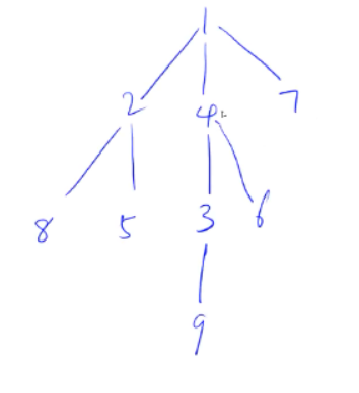
节点的编号是指上图所画的树中节点的值,范围是从1->n,编号用e[i]数组存储。
节点的下标指节点在数组中的位置索引,数组之间的关系就是通过下标来建立连接,下标用idx来记录。idx范围从0开始,如果idx==-1表示空。
e[i]的值是编号,是下标为i节点的编号。
ne[i]的值是下标,是下标为i的节点的next节点的下标。
h[i]存储的是下标,是编号为i的节点的next节点的下标,比如编号为1的节点的下一个节点是2,那么我输出e[h[1]]就是2。
链式前向星是一种常用的图存储方式,其主要优点如下:
1. 空间利用率高:链式前向星只需存储边信息,相对于邻接矩阵等其他图存储方式,可以大大节约空间。
2. 支持动态图:链式前向星在插入和删除边时具有较好的效率,支持实时更新图。
3. 方便遍历所有与某个点相邻的边:链式前向星通过一个数组来记录每个点最后一条边的位置,逐个遍历这些边即可找到所有与该点相邻的边。
4. 较好的灵活性和扩展性:链式前向星可以灵活地添加额外信息,比如权重、流量等,并且方便扩展到更复杂的图算法中。






