文章学习：TPRE：分布式门限代理重加密

学习文章：TPRE：分布式门限代理重加密

前言

成方金科新技术实验室与隐语团队合作，构建了“基于国密的分布式门限代理重加密算法TPRE”，为用户提供了一种安全、高效、自主可控的数据共享和授权管理方案。在数据隐私保护和数据安全共享方面具有广泛的应用前景。

??：该算法由成方金科密码学研究员张曙光（知乎：六三）基于隐语的密码库yacl实现，其提供了易于开发的密码工具接口，TPRE算法目前已经贡献至yacl中。https://github.com/secretflow/yacl/tree/main/yacl/crypto/primitives/tpre

TPRE算法具有以下优势：

• 数据密钥隐含在TPRE的密文中，无需对数据密钥进行管理，降低密钥管理的复杂度；
• 实现了数据的动态授权和访问控制；
• 适应于区块链中的分布式计算和数据安全共享场景，可以适配于未来价值网络Web 3.0；
• 使用国密算法SM2 、SM3和SM4对国际密码算法进行替换，实现自主可控。
• 替代了UMBRAL重加密方案

基础知识

代理重加密

代理重加密是一种公钥密码方案，它允许代理将一个公钥加密成的密文转换到另一个公钥加密成的密文，而代理者不能了解关于原始消息的任何信息，要做到这一点，代理必须拥有一个重加密密钥。

一个代理重加密算法通常包含三种角色，即数据拥有者Alice、数据接收者Bob和代理计算Proxy。

假设，数据\(m\)已经被Alice使用自己公钥加密为密文\(c\)，并存储在Proxy，具体算法具体步骤如下：

• Alice作为数据拥有者，想要将数据授权给Bob使用，则为Proxy生成重加密密钥\(rk\)。

• Proxy在接收到\(rk\)后，对密文\(c\)重加密，得到新密文\(c^‘\)，并将其发送至Bob。

• Bob使用自己的私钥\(c^‘\)对解密，即可得到明文数据\(m\)。

这里想起来了一个基于NTRU的代理重加密方案：NTRUReEncrypt: An Efficient Proxy Re-Encryption Scheme Based on NTRU，下面具体介绍一下方案：

代理重加密方案：NTRUReEncrypt

委托人为：A，被委托人为：B，代理者：proxy

• 密钥生成：A的密钥\((pk_A,sk_A)\)和B的密钥\((pk_B,sk_B)\)，以A的密钥生成为例：
  • A随机式生成一对多项式\((f_A,g_A)\in R^2_{NTUR}\)，系数为\((-1,0,1)\)，其中\(f_A \equiv 1 mod p\)；
  • 私钥\(sk_A=f_A\)，公钥为\(pk_A=h_A=p*g_Af_A^{-1} mod q\)；
• 重加密密钥生成\((sk_A,sk_B)\)
  • 输入A和B的私钥：\(sk_A=f_A\)和\(sk_B=f_B\)；
  • A、B和代理者proxy之间通过一个简单的三方协议计算出重加密密钥\(rk_{A\to B}\)：
    • A选择一个随机数\(r\in R_{NTRU/q}\)；
    • A计算\(r*f_A mod q\)并发送给B，A发送\(r\)给代理者proxy；
    • B计算\(r*f_A f_B^{-1} mod q\)给proxy；
    • 这样就能计算出\(rk_{A \to B}=f_A*f_B^{-1} mod q\)；
• 加密\((pk_A,M)\)
  • 输入公钥\(pk_A\)和消息\(M\in R_{NTRU/q}\)；
  • 随机选择一个多项式\(s\in R_{NTRU}\)；
  • 输出密文\(C_A=h_As+M\)；
• 重加密\((rk_{A\to B},C_A)\)
  • 输入重加密密钥\(rk_{A \to B}\)和密文\(C_A\)
  • 随机选择一个多项式\(e\in R_{NTRU}\)；
  • 输出新的密文\(C_B=C_A*rk_{A \to B}+pe\)；
• 解密\((sk_A,C_A)\)
  • 输入私钥\(sk_A=f_A\)和密文\(C_A\)；
  • 计算\(C_A^‘=(C_A*f_A) mod q\)；
  • 输出\(M=(C_A^‘ mod p)\)；
• 正确性证明：
  • A加密消息\(M\)，得到密文\(C_A\)，并生成重加密密钥\(rk_{A\to B}\)
  • 代理者proxy对密文\(C_A\)进行重加密，得到\(C_B=C_A*rk_{A\to B}+pe=(h_As+M)rk_{A\to B}+pe=pg_Af_B^{-1}s+pe + f_Af_B^{-1}M\)
  • B对\(C_B\)进行解密，计算\((C_B*f_B)mod q=((pg_Af_B^{-1}s+pe + f_Af_B^{-1}M)\cdot f_B)mod q=(pg_As + pe f_B + f_AM)mod q=M\)

分布式门限代理重加密

代理重加密适合在云计算场景中使用，即代理节点为计算性能较强的单节点，这与现有隐私计算体系架构不符，因为现在隐私计算架构通常是分布式架构。因此，需要对传统代理重加密方案进行改造，使之能够适应分布式计算环境。

分布式代理重加密是指将传统代理重加密中的单Proxy节点，拆分为多个Proxy节点。因而在对数据重加密时，需要多个Proxy节点参与合作计算。

考虑到选取参与计算的Proxy节点的灵活性，需要将分布式代理重加密重新设计为基于门限的分布式代理重加密。

Shamir Secret Sharing

Shamir Secret Sharing是一种加密技术，可以将秘密信息分散成多个部分，并分配给不同的人，只有所有部分被汇集在一起才能重构出原来的秘密信息。它是由以色列密码学家Adi Shamir在1979年发明的，被广泛应用于保护机密信息，例如在密码学、数字签名、多方计算等领域。其基本思想是通过多项式插值来实现信息的分散和重构，具有高度的安全性和可靠性。

Shamir密秘分享：假设有一个秘密信息，例如一个密码或者一个私钥，需要将这个秘密信息分配给两个人，可以使用Shamir Secret Sharing算法来实现。

• 首先，选择一个大的质数\(p\)，并选择一个阈值\(k\)，使得只有\(k\)个或更多的部分才能恢复原始秘密信息，这里\(k=2\)
• 然后，随机生成一个多项式\(f(x)\)，其中\(f(0)\)等于秘密信息，其余系数都是随机数。每个人得到一个点\((x，f(x))\)，其中\(x\)是一个随机数，并且只有两个点都被收集到了，才能恢复原始秘密信息。如果只有一个点，那么无法恢复原始秘密信息

例如：假设秘密信息是密码“5”，需要将它分配给两个人。

• 选择一个质数\(p=11\)，并选择阈值\(k=2\)。
• 随机生成一个多项式\(f(x)=4x+5\)，其中\(f(0)=5\)，将多项式的系数分别分配给两个人，例如第一个人得到\((1，9)\)，第二个人得到\((2，2)\)。如果两个人都收集到了这两个点，那么可以使用拉格朗日插值法恢复原始的多项式\(f(x)\)，进而得到秘密信息“5”。

具体参考：https://www.cnblogs.com/pam-sh/p/17179097.html#shamir秘密分享

椭圆曲线

下图是我国商用密码SM2选定的素数域椭圆曲线"sm2p256v1"的参数选择：

更多可参考SM2国标：

密码哈希函数

使用的哈希算法构造如下：

\(h_x= (1 + Bignum(SM3(x)||SM3(SM3(x))) )mod n-1\)

其中\(n\)是椭圆曲线的阶，\(x\)是函数的输入

SM3套wa？

混合加密体制

由于公钥密码是运行在代数计算上的密码算法，其计算效率远低于对称密码，因此，在待加密数据量较大时，使用公钥密码直接对数据加密不是一个良好选择。在该场景中，可使用混合加密体制KEM/DEM：

• KEM是指密钥封装机制(Key-Encapsulation Mechanism)
• DEM是指数据封装机制(Data-Encapsulation Mechanism)，可以看做是对称加密方案。

这两个机制联合使用，可以提供数据的加解密效率，在密文需要传输时，也可降低通信开销。具体而言，DEM机制是用作保护原始数据，即使用对称加密算法，对原始数据进行加密保护；KEM是用作保护加密原始数据时所使用的对称密钥，使用公钥加密算法对对称密钥进行加密保护。

关于更多密钥封装可参考：密钥封装和公钥加密的联系和区别？

UMBRAL代理重加密算法

方案：https://github.com/nucypher/umbral-doc

UMBRAL是一个代理重加密方案（A THRESHOLD PROXY RE-ENCRYPTION SCHEME），根据一个密钥封装算法改进而来。Alice作为数据产生方，通过\(N\)个代理阶段的重加密机制可以将密文的解密权限委托给Bob，具体来说，Bob得到\((t,N)\)个节点重加密信息才能解密（恢复）出该明文。

代理重加密的使用场景：公共网络中任意数量的参与者实现私人数据共享，但不向中间实体（代理者）泄漏密钥信息。

UMBRAL是阈值代理重加密算法，是非交互式的、单向的，且在重加密后可以验证的，在阈值方面采用Shamir 秘密分享技术。

• 单向：重加密密钥是单向的
• 非交互式：在重加密密钥生成中不使用被委托人Bob的私钥，例如“NTRUReEncrypt”是交互式的。

算法介绍

一个代理重加密【Proxy Re-Encryption，PRE】算法的简易框架如下：

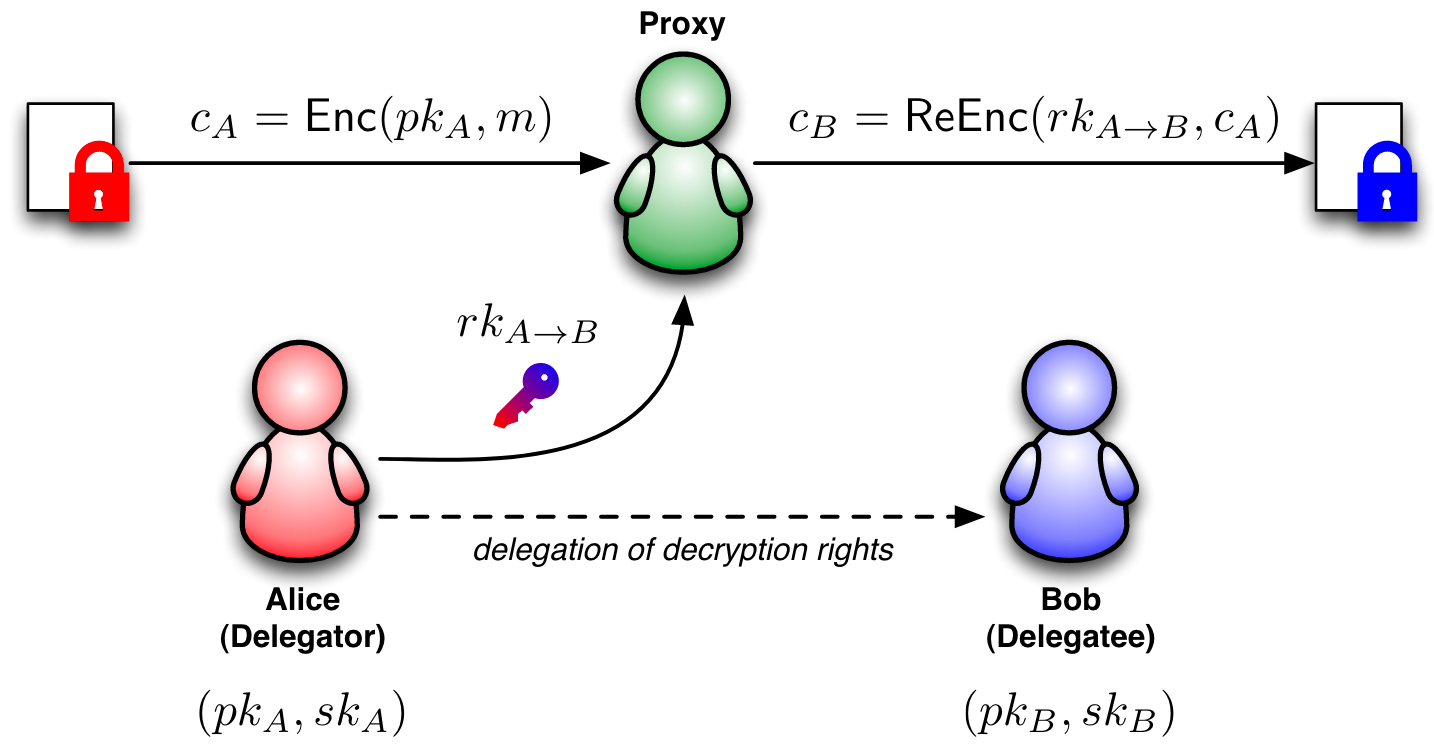
算法中用户角色主要有：

• Delegator【委托人】：Alice，加密明文消息，并生成一个重加密密钥，发送给代理者
• Delegatee【受委托人】：Bob，受Alice的委托用自己的私钥恢复明文，其中收到的密文是代理者重新加密后的
• Proxy【代理者】：将Alice发送来的密文利用重加密密钥重新加密，发送给Bob

代理重加密（PRE）由KEM（密钥封装）和DEM（分组加密）组成，其中DEM不涉及重加密，所以下图只讨论KEM部分。

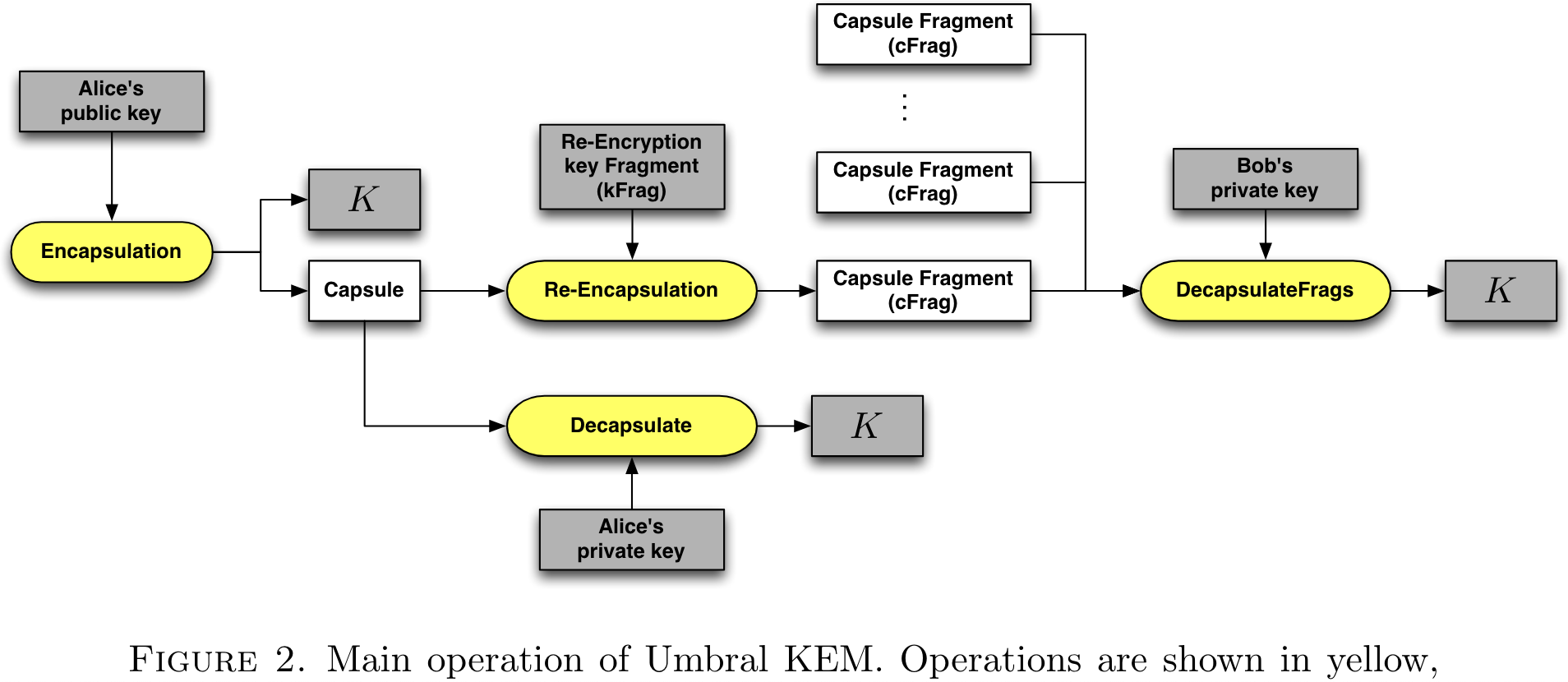
• Encapsulation：用Alice的公钥进行封装，得到密钥\(K\)和封装的密文\(capsule\)（胶囊）
• Decapsulate：用Alice的私钥进行解封装，获得密钥\(K\)
• Re-Encapsulation：Proxy使用重加密密钥片段对封装的密文进行再次封装，得到重封装的密文片段\(cFrag\)
• DecapsulateFrags：用Bob的私钥对重封装的密文片段进行接封装，得到密钥\(K\)

下面对KEM的算法功能模块分别介绍：

1、密钥生成算法

• 密钥生成\(KeyGen()\)

Alice得到一对公私钥对\((pk_A,sk_A)\)

• 重加密密钥生成\(ReKeyGen(sk_A,pk_B,N,t)\)

输入：\(sk_A=a\)、\(pk_B=g^b\)、片段\(N\)、阈值\(t\)

输出：\(N\)个重加密密钥片段\(kFrag\)

2、封装和解封装算法

• 封装\(Encapsulate(pk_A)\)

输入：\(pk_A\)

输出：对称加密密钥\(K\)和封装结果\(capsule\)

• 解封装\(Decapsulate(sk_A,capsule)\)

输入：\(sk_A\)和\(capsule\)

输出：对称加密密钥\(K\)

3、重封装和解封装片段算法

• 重新封装\(ReEncapsulation(kFrag,capsule)\)

输入：重加密密钥片段\(kFrag\)和封装结果\(capsule\)

输出：重新封装的片段（部分）\(cFrag\)

• 解封装片段\(DecapsulateFrags(sk_B,\left \{cFage_i \right \}_{i=1}^{t},capsule)\)

输入：Bob的私钥\(sk_B=b\)、\(t\)个重封装片段\(cFrag\)

输出：对称加密密钥\(K\)

具体算法

下面详细介绍KDM算法流程：

1、参数设置

• \(Setup(sec)\)
  • 根据安全参数\(sec\)，确定一个阶数为素数\(q\)的循环群\(G\)，\(g,U\in G\)是群的生成元；
  • 哈希函数\(H_2:G^2\to Z_q\)，\(H_3:G^3\to Z_q\)，\(H_4:G^3*Z_q\to Z_q\)看作是随机预言机；
  • 密钥派生函数\(KDF:G\to \left \{0，1 \right \}^l\)也看作是随机预言机，其中\(l\)依赖于安全参数\(sec\)；
  • 最后得到一个公共参数集：\(\text { params }=\left(\mathbb{G}, g, U, H_{2}, H_{3}, H_{4}, \mathrm{KDF}\right)\)

2、密钥生成算法

• \(KeyGen()\)

  • 选择一个随机数\(a,b\in Z_q\)，计算\(g^a,g^b\)；
  • Alice和Bob的公私钥分别为：\((pk_A,sk_A)=(g^a,a)\)和\((pk_B,sk_B)=(g^b,b)\)

• \(ReKeyGen(sk_A,pk_B,N,t)\)

  • 选择一个随机数\(x_A\in Z_q\)，计算\(X_A=g^{x_A}\)；
  • 计算\(d=H_{3}\left(X_{A}, p k_{B},\left(p k_{B}\right)^{x_{A}}\right)\)，其中\(d\)是Bob的密钥和临时密钥对\((x_A,X_A)\)进行非交互DH的结果，使用该共享秘密信息使得方案的重加密密钥的生成为非交互式的；
  • 选择\(t-1\)个随机值\(f_i\in Z_q,i\in [1,t-1]\)，计算\(f_0=a*d^{-1} mod q\)；
  • 构建级数为\(t-1\)的多项式\(f(x)\in Z_q[x]\)，例如\(f(x)=f_0+f_1x+...+f_{t-1}x^{t-1}\)；
  • 计算\(D=H_6(pk_A,pk_B,pk_B^a)\)；
  • 设置\(KF=0\)，重复执行\(N\)次：
    • 选择随机值\(y,id\in Z_q\)，\(id\)表示代理节点的编号；
    • 计算\(s_x=H_5(id,D)\)和\(Y=g^y\)；
    • 计算\(rk=f(s_x)\)；
    • 计算\(U_1=U^{rk}\)；
    • 计算\(z_1=H_4(Y,id,pk_A,pk_B,U_1,X_A)\)和\(z_2=y-a\cdot z_1\)；
    • 定义一个重加密密钥片段为\(kFrag=(id,rk,X_A,U_1,z_1,z_2)\)；
    • \(KF=KF\cup\{kFrag\}\)
  • 最后输出重加密密钥\(KF\)

3、封装和解封装算法

• \(Encapsulate(pk_A)\)

  • 选择随机值\(r,u\in Z_q\)，计算\(E=g^r,V=g^u\)，然后计算\(s=u+r*H_2(E,V)\)；
  • 计算\(K=\textsf{KDF}((pk_A)^{r+u})\)；
  • \(capsule=(E,V,s)\)，叫做“胶囊”，可以反推出（解封装）\(K\)；
  • 最终输出\((K,capsule)\)；

• \(CheckCapsule(capsule)\)

  • 判断\(g^s\overset{?}{=}V\cdot E^{H_2(E,V)}\)是否成立；

• \(Decapsulate(sk_A,capsule)\)

  • 调用\(CheckCapsule(capsule)\)检查\(capsule\)的有效性；
  • 计算\(K=KDF((E,V)^a)\)，恢复出\(K\)；

4、重封装和解封装片段算法

• \(ReEncapsulation(kFrag,capsule)\)

  • 调用\(CheckCapsule(capsule)\)检查\(capsule\)的有效性；
  • 计算\(E_1=E^{rk},V_1=V^{rk}\)；
  • 输出\(cFrag=(E_1,V_1,id,X_A)\)；

• \(DecapsulateFrags(sk_B,\left \{cFrag_i \right \}_{i=1}^{t},capsule)\)

  • 其中\(cFrag_i=(E_1,V_1,id,X_A)\);
  • 计算\(D=H_6(pk_A,pk_B,pk_A^b)\)；
  • 对于\(S=\left \{s_{x,i} \right \}_{i=1}^t\)，计算\(s_{x,i}=H_5(id_i,D)\)；
  • 计算\(\lambda_{i,S}=\prod\limits_{j=1,j\neq i}^t\dfrac{s_{x,j}}{s_{x,j}-s_{x,i}}\)，\(E^{\prime}=\prod\limits_{i=1}^t(E_{1,i})^{\lambda_{i,S}}\)，\(V^{\prime}=\prod\limits_{i=1}^t(V_{1,i})^{\lambda_{i,S}}\)；
  • 计算\(d=H_3(X_A,pk_B,X_A^b)\)，其中使用\(kFrag\)进行重封装的\(KF\)的\(X_A\)是相同的；
  • 输出对称密钥\(K=\textsf{KDF}((E'\cdot V')^d)\)；

结合上述KEM算法，加入\(DEM\)后，封装和解封装算法变为了加密和解密算法，另外需后续验证，所以DEM具体为认证加密算法（AEAD），下面给出完整的KEM/DEM算法：

• \(Encrypt(pk_A,M)\)：

  • 计算\((K,capsule)=Encapsulate(pk_A)\)；
  • 加密：\(encData=AEAD(K,M)\)，其中\(M\)是明文信息，使用\(K\)为密钥进行对称加密；
  • 输出\(C=(capsule,encData)\)；

• \(Decrypt(sk_A,C)\)：

  • 计算\(K=Decapsulate(sk_A,cap sule)\)；
  • 解密：\(M=IAEAM(K,encData)\)；
  • 输出\(M\);

• \(ReEncrypt(kFrag,C)\)：

  • 计算\(cFrag=ReEncapsulation(kFrag,capsule)\)；
  • 输出\(C'=(cFrag,encData)\)；

• \(DecryptFrags(sk_B,\{C_i'\}_{i=1}^t)\)：

  • 其中\(C_i'=(cFrag_i,encData)\)；
  • 计算\(K=DecapsulateFrags(sk_B,\left \{cFrag_i \right \}_{i=1}^{t},capsule)\)
  • 计算\(M=IAEAM(K,encData)\)

正确性和安全性参考原文。

程序

源程序：https://github.com/nucypher/pyumbral

pyUmbral是对门限代理重加密方案Umbral的实现，基于python，依赖openssl和cryptography库。

在该程序中，Alice（数据拥有者）通过一个重加密的代理节点，将解密权利授权给Bob。具体说，当有门限个代理节点参与重加密时，Bob能聚合这些重加密的密文，然后使用自己的私钥解密恢复出原始消息。

pyUmbral是nucypher背后的加密引擎，nucypher是一个代理重新加密网络，用于在去中心化系统中增强隐私。

安装

pip3 install umbral

使用

下面以一个例子证明方案功能的正确性（docs/examples/umbral_simple_api.py）：

1、密钥生成

• Alice生成：

  • 加密公私钥对（alices_public_key，alices_secret_key）
  • 签名公私钥对（alices_verifying_key，alices_signing_key）

• Bob生成：

  • 加密公私钥对（bobs_public_key，bobs_secret_key）

import random
from umbral import (
    SecretKey, Signer, CapsuleFrag,
    encrypt, generate_kfrags, reencrypt, decrypt_original, decrypt_reencrypted)

# Generate an Umbral key pair
# ---------------------------
# First, Let's generate two asymmetric key pairs for Alice:
# A delegating key pair and a Signing key pair.

alices_secret_key = SecretKey.random()                  #sk_A
alices_public_key = alices_secret_key.public_key()      #pk_A

alices_signing_key = SecretKey.random()                 #签名私钥
alices_verifying_key = alices_signing_key.public_key()  #签名公钥
alices_signer = Signer(alices_signing_key)
  
bobs_secret_key = SecretKey.random()            #sk_B
bobs_public_key = bobs_secret_key.public_key()  #pk_B

2、加解密

• Alice加解密测试：
  • 用公钥加密明文消息（Proxy Re-encryption is cool!）
  • 密文结构（capsule，ciphertext），其中ciphertext表示加密的密文，capsule表示胶（e,v,s）
  • 用私钥解密
• Bob测试：
  • 用私钥对密文解密，解密错误！

# Encrypt some data for Alice
# ---------------------------
# Now let's encrypt data with Alice's public key.
# Invocation of `pre.encrypt` returns both the `ciphertext`,
# and a `capsule`. Anyone with Alice's public key can perform
# this operation.

plaintext = b'Proxy Re-encryption is cool!'
capsule, ciphertext = encrypt(alices_public_key, plaintext)
print("ciphertext:",ciphertext)

# Decrypt data for Alice
# ----------------------
# Since data was encrypted with Alice's public key,
# Alice can open the capsule and decrypt the ciphertext with her private key.

cleartext = decrypt_original(alices_secret_key, capsule, ciphertext)
print("cleartext:",cleartext)
  
# Bob receives a capsule through a side channel (s3, ipfs, Google cloud, etc)
bob_capsule = capsule

# Attempt Bob's decryption (fail)
try:
    fail_decrypted_data = decrypt_original(bobs_secret_key, bob_capsule, ciphertext)
except ValueError:
    print("Decryption failed! Bob doesn't has access granted yet.")

3、重加密

• Alice生成重加密密钥：
  • 根据Alice的私钥、Bob的公钥、签名信息
  • 产生20个重加密密钥
• 代理节点：
  • 从20个中选出10个重加密密钥（kfrags）
  • 使用kfrags对capsule重加密得到重加密后的密文（cfrags）

# Alice grants access to Bob by generating kfrags
# -----------------------------------------------
# When Alice wants to grant Bob access to open her encrypted messages,
# she creates *threshold split re-encryption keys*, or *"kfrags"*,
# which are next sent to N proxies or *Ursulas*.
# She uses her private key, and Bob's public key, and she sets a minimum
# threshold of 10, for 20 total shares

kfrags = generate_kfrags(delegating_sk=alices_secret_key,
                         receiving_pk=bobs_public_key,
                         signer=alices_signer,
                         threshold=10,
                         shares=20)                     #Alice产生20个重加密密钥片段，给代理节点

# Ursulas perform re-encryption
# ------------------------------
# Bob asks several Ursulas to re-encrypt the capsule so he can open it.
# Each Ursula performs re-encryption on the capsule using the `kfrag`
# provided by Alice, obtaining this way a "capsule fragment", or `cfrag`.
# Let's mock a network or transport layer by sampling `threshold` random `kfrags`,
# one for each required Ursula.

kfrags = random.sample(kfrags,  # All kfrags from above
                       10)      # M - Threshold         #从20个重加密密钥片段中，随机选出10个用作重加密

# Bob collects the resulting `cfrags` from several Ursulas.
# Bob must gather at least `threshold` `cfrags` in order to open the capsule.

cfrags = list()  # Bob's cfrag collection
for kfrag in kfrags:
    cfrag = reencrypt(kfrags=capsule, kfrag=kfrag)
    cfrags.append(cfrag)  # Bob collects a cfrag

assert len(cfrags) == 10

4、解密

• Bob先验证capsule的合法性
  • 使用Alice的公钥、Bob的公钥和Alice的签名公钥
• Bob解密：
  • 使用Bob的私钥、Alice的公钥、重加密后的密文（cfrage）、capsule和ciphertext

# Bob checks the capsule fragments
# --------------------------------
# If Bob received the capsule fragments in serialized form,
# he can verify that they are valid and really originate from Alice,
# using Alice's public keys.

suspicious_cfrags = [CapsuleFrag.from_bytes(bytes(cfrag)) for cfrag in cfrags]

cfrags = [cfrag.verify(capsule,
                       verifying_pk=alices_verifying_key,
                       delegating_pk=alices_public_key,
                       receiving_pk=bobs_public_key,
                       )
          for cfrag in suspicious_cfrags]               #验证重加密后的密文

# Bob opens the capsule
# ------------------------------------
# Finally, Bob decrypts the re-encrypted ciphertext using his key.

bob_cleartext = decrypt_reencrypted(receiving_sk=bobs_secret_key,
                                    delegating_pk=alices_public_key,
                                    capsule=bob_capsule,
                                    verified_cfrags=cfrags,
                                    ciphertext=ciphertext)  #Bob使用sk_B解密得到明文
print("bob_cleartext:",bob_cleartext)
assert bob_cleartext == plaintext

TPRELib算法

介绍

TPRELib共包含6个算法，分别为密钥对生成算法【GenerateTpreKeyPair】、重加密密钥生成【GenerateReKey】、加密【Encrypt】、解密算法【Decrypt】、重加密算法【ReEncrypt】、解密重加密密文算法【DecryptFrage】：

假设数据持有方为A，接收方为B，代理者（节点）为proxy

• \(\mathop{\mathrm{GenerateTpreKeyPair}}(\lambda)\to(p k_{A},s k_{A})\)：输入安全参数\(\lambda\)，A和B各自生成公私钥对\((pk_A,sk_A)\)和\((pk_B,sk_B)\)；
• \(\text{}\mathrm{GenerateReKey}(sk_A,pk_B,N,t)\to(\{rk_i\},i\in[1,N])\)：输入A的私钥\(sk_A\)，B的公钥\(pk_B\)，所有代理节点数量\(N\)和门限\(t\)，输出重加密密钥集合\(rk_i(i\in[1,N])\)。这里的\(i\)是指代理节点的ID；
• \(\text{Encrypt}(pk_A,m)\to c\)：输入A的公钥\(pk_A\)和明文\(m\)，输出密文\(c\)；
  • 这里并不是直接使用\(pk_A\)加密明文，因为会导致性能过低问题，在底层加密时，使用的是对称加密算法，在本库中对称加密算法由SM4实现，其对称密钥是在加密过程中随机产生，对称加密密钥由公钥加密保护【明文使用SM4加密，\(pk_A\)加密对称加密的密钥】
  • 生成对称密钥时，需要用到密码哈希函数构建的密钥派生函数KDF（Key derivation function），本库使用SM3代替SHA-2等国际算法，实现该KDF函数。【可以实现指定长度的哈希字符串】
• \(\operatorname{Decrypt}(sk_A,c)\to m\)：输入A的私钥\(sk_A\)和密文\(c\)，输出明文\(m\)；
  • 这里是和加密算法是逆过程，即用\(sk_A\)解密得到对称加密密钥，再解密密文
• \(\text{ReEncrypt}(rk_i,c)\to c'_i\)：代理节点输入重加密密钥\(rk_i\)和密文\(c\)，输出新密文\(c_{i}^{\prime}\)；
• \(\text{DecryptFrage}(c_{i}^{\prime}(i\in[t,N]),sk_{B})\rightarrow m\)：输入的是门限个数的新密文集合\(c_{i}^{\prime}(i\in[t,N])\)和接收方的私钥\(sk_{B}\)，输出明文\(m\)

下面是门限代理重加密算法执行流程：

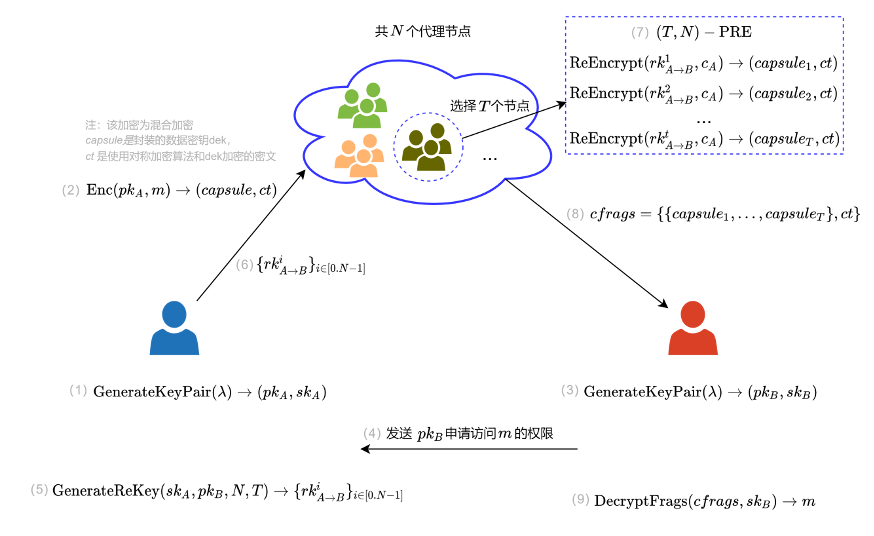
\(capsule\)：包含对称密钥信息

\(ct\)：使用对称加密的密文

具体算法

参数设置

假设Alice为数据所有方，Bob为数据需求方，代理者（代理节点）为proxy

设置参数，为了简单起见，我们将省略其余函数中的公共参数。

• \(Setup(sec)\)：首先根据安全参数\(sec\)确定一个素数\(q\)的循环群\(G\) ，让\(g,U\in G\)是生成元。
  • \(H_2:G^2\to Z_q\)、\(H_3:G^3\to Z_q\)和\(H_4：G^3\to Z_q\)表示密码哈希函数（假设把它们当做随机预言机）
  • \(KDF:\to \left \{ 0,1 \right \} ^l\)是一个同样作为随机预言机的密钥衍生函数，其中\(l\)是安全参数 。
  • 全局公共参数由以下元组表示：\(\mathit{p a r a m s} m s=(\mathbb{G},g,U,H_{2},H_{3},H_{4},\mathrm{KDF})\)

密钥对生成

• \(KeyGen()\): Alice在\(Z_q\)中均匀地随机选择\(a\)，即\(a\in Z_q\)，计算\(g^a\)并输出Alice的密钥对\((pk_A,sk_A)=(g^a,a)\)，Bob同样输出密钥对\((pk_B,sk_B)=(g^b,b)\)

重加密密钥生成

• \(ReKeyGen(sk_A,pk_B,N,t)\)：输入\((pk_A,sk_A)\) ，\(pk_B\)，代理节点数\(N\)和阈值\(t\)，重加密密钥生成算法计算出Alice和Bob之间的\(N\)个代理节点的重加密密钥:

  • 随机抽样\(x_A\in Z_q\)并计算\(X_A=g^{x_A}\)

  • 计算\(d=H_3(X_A,pk_B,(pk_B)^{x_A})=H_3(g^{x_a},g^b,g^{bx_a})\)

    • \(d\)是Bob的密钥对与临时密钥对\((x_A,X_A)\)的非交互式Diffie-Hellman密钥交换的结果，我们将使用这个共享的密钥来使该方案的重加密密钥生成变为非交互式

  • 在\(f_i\in Z_q\)中随机抽取\(t-1\)个元素，其中\(i\in [1,t-1]\)，并计算\(f_0=(a*d^{-1}) mod q\)

  • 【密秘分享】在\(r-1\)阶的\(Z_q[x]\)中构造一个多项式\(f(x)\) ，使得\(f(x)=f_0+f_1x+f_2x^2+...+f_{t-1}x^{t-1}\)

  • 计算\(D=H_6(pk_A,pk_B,pk_B^a)=H_6(g^a,g^b,g^{ba})\)

  • 初始化集合\(KF=0\)，重复\(N\)次

    • 随机选取\(y\in Z_q\)，计算\(Y=g^y\)
    • 计算\(s_x=H_5(id,D)\)，其中\(id\)是代理节点的ID
    • 计算\(rk=f(s_x)\)，计算\(U_1=U^{rk}\)
    • 定义一个重加密密钥片段\(kFrag=(id,rk,X_A,U_1)\)
    • \(KF=KF\cup kFrag\)
    • 最后输出重加密密钥片段\(KF\)

• 封装算法\(Encapsulate(pk_A)\)：输入公钥\(pk_A=g^a\)

  • 首先选择随机数\(r,u\in Z_q\) ，并计算\(E=g^r\)和\(V=g^u\)

  • 计算\(s=u+r*H_2(E,V)\)，计算\(K=KDF((pk_A)^{r+u})=KDF(g^{a(r+u)})\)，该元组\((E,V,s)\)被称为胶囊（capsule）

  • 最后输出\((K,capsule)\)，其中\(K\)为对称密钥

• 检查函数\(CheckCapsule(capsule)\)：在输入一个\(capsule=(E,V,s)\)时，通过检查以下方程是否成立来检查该胶囊的有效性：\(g^{s}\overset{?}{=}V\cdot E^{H_{2}(E,V)}\)

• 解封算法\(Decapsulate(sk_A,capsule)\)：输入密钥\(sk_A=a\)和原始胶囊\(capsule=(E,V,s)\)

  • 首先用CheckCapsule检查胶囊的有效性，如果检查失败，则输出\(\bot\)，否则计算\(K=KDF((E*V)^a)=KDF(g^{a(u+r)})\)
  • 最后输出\(K\)

封装算法是根据公钥\(pk_A\)生成一个对称密钥\(K\)和一个capsule

解封装算法可以根据capsule还原出对称密钥\(K\)

• 重封装算法\(ReEncapsule(kFrag,capsule)\)：输入一个重加密的密钥片段\(kFrag=(id,rk,X_A,U_1)\)和一个\(capsule=(E,V,s)\)
  • 首先用CheckCapsule检查胶囊的有效性，如果检查失败，则输出\(\bot\)，否则计算\(E_1=E^{rk}\)和\(V_1=V^{rk}\)，并输出胶囊片段\(cFrag=(E_1,V_1,id,X_A)\)
• 解封装密钥算法\(DecapsuleFrags(sk_B,pk_A,\left \{ cFrag_i \right \}_{i=1}^t )\)：输入密钥\(sk_B=b\)，原始公钥\(pk_A=g^a\)和\(t\)个胶囊片段，每个片段为\(c F r a g_{i}=\left(E_{1,i},V_{1,i},i d_{i},X_{A}\right)\)：
  • 计算\(D=H_0(pk_A,pk_B,pk_A^b)\)
  • \(\begin{aligned}& \\&S=\left(\{s_{x,i}\}_{i=1}^{t}\right)\end{aligned}\)，其中\(s_{x,i}=H_5(id_i,D)\)，对于\(s_{x,i}\in S\)，计算\(\lambda_{i,S}=\prod\limits_{j=1,j\neq i}^t\dfrac{s_{x,j}}{s_{x,j}-s_{x,i}}\)
  • 计算\(E'=\prod\limits_{i=1}^t(E_{1,i})^{\lambda_{i,s}}\)和\(V'=\prod\limits_{i=1}^t(V_{1,i})^{\lambda_{i,S}}\)
  • 计算\(d=H_{3}\bigl(X_{A},p k_{B},X_{A}^{b}\bigr);\)
    • \(d\)的\(B\)是密钥对和临时密钥对\((x_A,X_A)\)之间非交互式Diffie-Hellman密钥交换的结果。对于所有的\(cFrags\)来说，其值是相同的，这些\(cFrags\)是通过使用重加密密钥片段集\(KF\)中的\(kFrag\)产生的。
  • 最后输出对称密钥\(K=\mathrm{KDF}{\Big(}\left(E^{\prime}\cdot V^{\prime}\right)^{d}{\Big)}\)

数据加密

• \(\operatorname{Encrypt}(p k_A,M)\)：在输入公钥\(pk_A\)和信息\(M\)时，加密算法首先计算\((K,capsule)=\operatorname{Encapsulate}(pk_A)\)，其中\(encData\)是用密钥\(K\)对\(M\)应用AEAD的结果，\(capsule\)是相关数据
• 最后输出密文\(C=(c a p s u l e,e n c D a t a)\)

数据解密

• \(\operatorname{Decrypt}(sk_A,C)\)：在输入秘密密钥\(sk_A\)和密文\(C\)时，解密算法计算出密钥\(K=\mathrm{Decapsulate}(s k_{A},c a p s u l e)\)，并使用AEAD的解密函数对密码文本\(encData\)进行解密，如果解密正确，则得到消息\(M\)，否则得到\(\bot\) ，最后输出消息\(M\)（如果解密无效则输出\(\bot\)）。

数据密文重加密

• \(\mathrm{ReEncrypt}(kFrag,C)\)： 在输入一个重加密的密钥片段\(kFrag\)和一个密文\(C\)时，重加密算法对\(capsule\)应用\(Recapsulate\)以获得\(cFrag\)，并输出重加密的密文\(C'=(cFrag,encData)\)

数据重加密密文解密

• \(\operatorname{DecryptFrags}\Big(sk_B,\Big\{C_i^{prime}\Big\}_{i=1}^t\Big)\)。在输入\(sk_B\)时，一组\(t\)个重加密的密文\(\begin{gathered} C_i' = (cFrag_i,encData) \\\end{gathered}\)，片段解密算法首先用\(\begin{aligned}& \\&\mathrm{DecapsulateFrags}\Big(s_{B},\{c F r a g_{i}\}_{i=1}^{t}\Big) \\&\end{aligned}\)对\(cFrag\)进行解密，产生密钥\(K\)，并使用AEAD的解密函数对密码文本\(encData\)进行解密，密钥\(K\)和胶囊作为相关数据，如果解密正确，则得到消息\(M\)，否则得到\(\bot\)。最后它输出消息\(M\)（如果解密无效，则输出\(\bot\)），其中对称密文\(encData\)对于所有的\(C_i^‘\)都是相同的密文\(C\)的重加密

安全性

椭圆曲线安全性

本算法可以选择任意素数域椭圆曲线，例如Secp256k1和sm2p256v1，其中sm2p256v1是我国国产密码学算法SM2使用的椭圆曲线【2.4】

数据密钥的安全性

• 数据密钥随机性：数据密钥的随机性由随机数\(pk_A,r,u\)决定，其中\(pk_A=g^a,sk_A=a\in Z_q,r,u\in Z_q\)
• 数据密钥的保密性：数据密钥由公钥密码保护，公钥密码建立在椭圆曲线离散对数困难问题之上
• 整个算法中使用的密码哈希函数、密钥派生函数来源于我国商用密码SM3
• 整个算法中使用的对称加密算法来源于我国商用密码SM4

程序

源程序：https://github.com/secretflow/yacl/tree/main/yacl/crypto/primitives/tpre

介绍

TPRE是umbral的替代品，它是用C++实现的，用SM2、SM3和SM4取代了ECC和AES等算法。

可用于一下场景：

• 数据安全共享

• 数据安全授权

• 分布式密钥管理

模块功能：

• Hash.h/hash.cc：使用的哈希函数，封装了SM3
• kdf.h/kdf.cc：使用的KDF，使用了SM3
• Keys.h/keys/cc：库中提供密钥生成和重加密密钥生成
• Capsule.h/capsule. cc：重加密的实现
• tpre.h/tpre.cc：加密、解密、重加密等

安装

由于tpre是放在隐语的yacl库中，安装编译参考“yacl使用”

使用

1、密钥生成

• 生成曲线参数
• Alice和Bob各自生成密钥对
• 使用Alice的密钥对和Bob的公钥生成重加密密钥

std::unique_ptr<EcGroup> ecc_group = EcGroupFactory::Create("sm2");       //初始化参数，生成SM2对应的曲线参数

Keys keys;
std::pair<Keys::PublicKey, Keys::PrivateKey> key_pair_alice =                 
    keys.GenerateKeyPair(ecc_group);

// According to the official SM2 document
// The hexadecimal of generator is:
// Gx = 32C4AE2C 1F198119 5F990446 6A39C994 8FE30BBF F2660BE1 715A4589
// 334C74C7
// Gy = BC3736A2 F4F6779C 59BDCEE3 6B692153 D0A9877C C62A4740 02DF32E5
// 2139F0A0

// When converting it to decimal, we have :
// "(2296314654723705055947953136255007457880
// 2567295341616970375194840604139615431,
// "85132369209828568825618990617112496413088
// 388631904505083283536607588877201568)";

std::string generator_str =
    "(2296314654723705055947953136255007457880256729534161697037519"
    "4840604139"
    "615431, "
    "85132369209828568825618990617112496413088388631904505083283536"
    "6075888772"
    "01568)";
EXPECT_EQ(ecc_group->GetAffinePoint(key_pair_alice.first.g).ToString(),
          generator_str);                                                 //检测generator_str点是否在曲线上

std::pair<Keys::PublicKey, Keys::PrivateKey> key_pair_bob =
    keys.GenerateKeyPair(ecc_group);                                      //Bob生成一对公私钥

std::vector<Keys::KFrag> kfrags =
    keys.GenerateReKey(ecc_group, key_pair_alice.second, key_pair_alice.first,
                       key_pair_bob.first, 5, 4);                         //生成5个重加密密钥

for (int i = 0; i < 5; i++) {
  EXPECT_TRUE(kfrags[i].id > zero);
}

2、加解密

• Alice生成公私钥
• Alice加解密测试

/************************* Phase 1 *************************/
// Start testing encryption and decryption functions
std::unique_ptr<EcGroup> ecc_group = EcGroupFactory::Create("sm2");       // 参数生成

std::pair<Keys::PublicKey, Keys::PrivateKey> key_pair_A =
    keys.GenerateKeyPair(ecc_group);                                      //Alice生成密钥对

// test tpre.Encrypt
std::string message = "hellooooooooooooo, I am 63, who are you?";         //明文消息

std::pair<Capsule::CapsuleStruct, std::vector<uint8_t>> ct_1 =
    tpre.Encrypt(ecc_group, key_pair_A.first, iv, message);               //使用Alice的公钥加密得到密文（Capsule，encdata）

// test tpre.Decrypt

std::string message_1 =
    tpre.Decrypt(ecc_group, ct_1.first, iv, ct_1.second, key_pair_A.second);  //使用Alice的私钥解密得到明文

// Determine if decryption was successful
EXPECT_EQ(message, message_1);                                                //测试解密是否成功

// End testing encryption and decryption functions

3、重加密和解密

• Alice使用公钥加密消息
• 生成N个重加密密钥片段
• 选\(t\)个重加密密钥片段进行重新加密密文
• Bob使用私钥解密，恢复明文

/************************* Phase 2 *************************/
// Start testing encryption, re-encryption, and decryption functions

// Second test tpre.Encrypt
std::string message_2 =
    "If you were a teardrop;In my eye, For fear of losing you, I would never "
    "cry. And if the golden sun, Should cease to shine its light, Just one "
    "smile from you, Would make my whole world bright.";

std::pair<Capsule::CapsuleStruct, std::vector<uint8_t>> ct_2 =
    tpre.Encrypt(ecc_group, key_pair_A.first, iv, message_2);                  //使用Alice的公钥加密明文消息

// test keys->GenerateReKey
std::pair<Keys::PublicKey, Keys::PrivateKey> key_pair_B =
    keys.GenerateKeyPair(ecc_group);                                           //Bob生成公私钥

int N = 5;  // Number of all participants     //代理节点数
int t = 4;  // Threshold                      //阈值大小

std::vector<Keys::KFrag> kfrags = keys.GenerateReKey(
    ecc_group, key_pair_A.second, key_pair_A.first, key_pair_B.first, N, t);     //生成N个重加密密钥片段

// test tpre.ReEncrypt
std::pair<std::vector<Capsule::CFrag>, std::vector<uint8_t>> re_ct_set;

// You need to meet the number of participants to successfully decrypt,
// otherwise decryption will not be successful

for (int i = 0; i < t; i++) {
  std::pair<Capsule::CapsuleStruct, std::vector<uint8_t>> ct_2_i = {
      ct_2.first, ct_2.second};

  std::pair<Capsule::CFrag, std::vector<uint8_t>> re_ct_i =
      tpre.ReEncrypt(ecc_group, kfrags[i], ct_2_i);                               //使用重加密密钥片段 重新加密密文 得到re_ct_set

  std::unique_ptr<Capsule::CFrag> cfrag_i_up(
      new Capsule::CFrag(re_ct_i.first));

  re_ct_set.first.push_back(re_ct_i.first);

  re_ct_set.second = re_ct_i.second;
}

// test tpre.DecryptFrags

std::string message_3 =
    tpre.DecryptFrags(ecc_group, key_pair_B.second, key_pair_A.first,
                      key_pair_B.first, iv, re_ct_set);                           //Bob使用私钥解密

// Determine whether decryption was successful after performing re-encryption

EXPECT_EQ(message_2, message_3);

总结

为了适应数据要素化背景下数据流通需求场景，提出了基于国密的分布式门限代理重加密算法TPRE，该算法是由成方金科新技术实验室密码学研究员张曙光基于隐语社区的基础密码学库yacl实现。与传统的访问控制和权限管理方法相比，TPRE算法具有以下优点：

• 高强度加密：使用门限代理重加密技术对数据进行高强度加密，保护数据的机密性和隐私性。
• 分布式架构：采用分布式架构实现对分布式数据的访问控制和授权管理，解决了传统方法在分布式场景下的难题。
• 自主可控：基于国密算法设计，保证了数据的自主可控性，可以有效地避免数据泄露和信息安全风险。
• 高效性能：算法实现简单、计算量小，可在现有的计算资源下高效地进行数据安全共享和授权管理。

总之，基于国密的分布式门限代理重加密算法TPRE在数据隐私保护和数据安全共享方面具有广泛的应用前景和重要意义，为用户提供了一种安全、高效、自主可控的数据共享和授权管理方案。