第十四届蓝桥杯省赛C++ B组（个人经历 + 题解）

参赛感受

这是我第一次参加蓝桥杯的省赛，虽然没什么参赛经验，但是自己做了很多前几届蓝桥杯的题，不得不说，这一届蓝桥杯省赛的难度相较于之前而言还是比较大的。之前很流行蓝桥杯就是暴力杯的说法，但是随着参赛人数的增多，比赛认可度的提升，比赛题目的质量也明显越来越高了。这次省赛涉及知识点非常全面，而且难度都不小（题目涉及了暴力、模拟、数学、递归、动态规划、广度优先搜索、前缀和、最近公共祖先等）。总得来说，大概就是“你知道题目考的是什么，但是就是不太会做”。这也是我在比赛过程中的真实感受。

不过最后成绩还是不错的，拿了省一。我算了一下自己的分数，大概是50-60分，顶多也就是对了五道题的样子。我考完试都觉得可能完了，结果这个分数居然还能排在江苏省一的中游，看来我运气还是不错的哈哈哈。

时隔一个月，有些平台上已经有了第十四届蓝桥杯的题目，我打算记录一下自己参赛的经历并写下每道题的题解。
PS: 本博客中编程题的代码都是在Acwing平台上提交且通过的代码。

---

A：日期统计 暴力枚举

解题思路

第一道题是一个填空题，大致意思就是一个由100个数字组成的序列，统计符合"\(2023mmdd\)"格式的无重复子序列的个数，"\(2023mmdd\)"表示一个2023年的一个合法的日期，其中"\(mm\)"表示月份的两位数字，"\(dd\)"表示天数的两位数字。

我一开始有点不敢写暴力，毕竟要八重循环呢！后来发现前四重循环在判断年份的时候，由于年份确定为"2023"，故只需要判断当前循环是否符合即可，如果不符合，就跳过这一整层的循环，比如说第一层循环，只需要判断是否等于2就行，如果胡等于2，就跳过。这样前面四重循环可以节省大量的运行时间，整个八重循环基本上就变成一个四重循环了，总共就100个数，所以可以在一秒左右的时间就跑出结果。

对于判重，我使用的是\(set\)，每出现一个合法日期，用 \(月份 × 100 + 天数\) 设为对应哈希值，放入\(set\)中。最后返回\(set\)的大小即答案。

答案： 235

个人战况

这道题做出来了，但是消耗了很多时间，一直不敢写暴力，自己在考场上可能也有紧张的因素，而且我一直都喜欢睡懒觉，所以上午做题可能多少也影响到我的状态了哈哈哈。幸好最后还是做出来了。

代码

#include<iostream>
#include<string>
#include<set>
using namespace std;

const int N = 110;
int num[N];
set<int> st;    //利用set去重
int day[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	for(int i = 0; i < 100; i ++ ) cin >> num[i];   //输入数据

	for(int y1 = 0; y1 < 100; y1 ++ ){
		if(num[y1] != 2) continue;
		for(int y2 = y1 + 1; y2 < 100; y2 ++ ){
			if(num[y2] != 0) continue;
			for(int y3 = y2 + 1; y3 < 100; y3 ++ ){
				if(num[y3] != 2) continue;
				for(int y4 = y3 + 1; y4 < 100; y4 ++ ){
					if(num[y4] != 3) continue;
					
					//判断月份和天数
					for(int m1 = y4 + 1; m1 < 100; m1 ++ )
						for(int m2 = m1 + 1; m2 < 100; m2 ++ )
							for(int d1 = m2 + 1; d1 < 100; d1 ++ )
								for(int d2 = d1 + 1; d2 < 100; d2 ++ ){
									int m = num[m1] * 10 + num[m2], d = num[d1] * 10 + num[d2];
									if(m >= 1 && m <= 12 && d >= 1 && d <= day[m]){
										int res = m * 100 + d;   //月份成100 + 天数设为对应哈希值
										st.insert(res);
									}
								}
				}
			}
		}
	}

	cout << (int)st.size() << endl;

	return 0;
}

---

B：01串的熵 套公式 + 暴力枚举

解题思路

题目大致意思就是给一个信息熵的公式，然后现在给你一个信息熵的值和字符串的长度，且字符串中只有0和1，由此逆推0出现的次数。

这道题给出的定义和公式看起来有点吓人，然而字符串中只有0和1两种字符，所以只要枚举套公式求解即可。

答案：11027421

个人战况

这道题还挺简单的，但是我被第一道题给影响到了，毕竟我第一道题都花了很多时间，然后一看第二个填空题，给了个看起来很复杂的公式，一下子不知道怎么去做，然后当时就跳过了这道题。虽然分值只有五分，但是还是很可惜的，没能做这道简单的填空题。

代码

#include<iostream>
#include<cmath>
using namespace std;

const double eps = 1e-4;
const int N = 23333333;

//填入公式
bool check(int n0){
	int n1 = N - n0;
	double p0 = n0 * 1.0 / N, p1 = n1 * 1.0 / N;
	double res1 = n0 * p0 * log(1.0 / p0) / log(2);
	double res2 = n1 * p1 * log(1.0 / p1) / log(2);

	return fabs(res1 + res2 - 11625907.5798) <= eps;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	//枚举0出现的次数
	for(int i = 0; i < (N >> 1); i ++ )
		if(check(i)) {
			cout << i << endl;
			break;
		}

	return 0;
}

---

C：冶炼金属 找规律 + 数学

解题思路

题目大致意思就是，给出若干组 \(a\) 和 \(b\)，其中 \(a\) 是使用的金属原料的数量，\(b\) 是消耗 \(a\) 个原料最多可以得到的新金属的数量。假设每得到一个新金属需要消耗 \(v\) 个原料，这道题要确定的就是 \(v\) 的范围，即 \(v\) 的最小可能值和最大可能值。

这本质上是一个数学题，通过找规律可以发现，\(v\) 的最大可能值，即所有 \(?a/b?\) 的最小值；\(v\) 的最小可能值，是所有 \(?a/(b+1)? + 1\) 的最小值。

此结论也可以通过推公式来得到：
假设每得到一个新金属需要消耗 \(v\) 个原料，消耗 \(a\) 的原料得到 \(b\) 个新金属，但是无法得到 \(b + 1\) 个新金属，所以 \(b \times v\le a< (b+1)\times v\)

由此可得：\(\frac{a}{b+1} < v\le \frac{a}{b} \)

由于 \(v\) 是整数，所以最小值为 \(\frac{a}{b+1} + 1\)，最大值为 \(\frac{a}{b}\) 。

个人战况

这道题应该是拿了全分的，不过考试的时候一直在找规律，处理整除操作上的细节，没有直接从数学的角度去推导公式，所幸最后还是做出来了。

代码

#include<iostream>
#include<cmath>
using namespace std;

int maxv = 1e9, minv;  //maxv确定最大值上限 minv确定最小值下限

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    
    int a, b, n; cin >> n;
    while(n -- ){
        cin >> a >> b;
        maxv = min(maxv, a / b);
        minv = max(minv, a / (b + 1) + 1);
    }
    
    cout << minv << ' ' << maxv << endl;
    
    return 0;
}

---

D：飞机降落 全排列 + 贪心

解题思路

题目大致意思是给定 \(n\) 架飞机的最早降落时间 \(t\)，盘旋时间 \(d\) 以及降落所需时间 \(l\)，每架飞机从开始降落到降落结束过程中，其它飞机都不能降落，通俗得说就是这段时间里空中只有这一架飞机正在降落。求是否存在一种排列方案，使得所有飞机都可以降落到地面。

这道题本质上就是一个求不相交区间的问题，我一开始想到的是纯贪心，考试的时候，我通过直觉判断用最晚降落时间\(t + d\)进行升序排序，这样的容错率感觉会更高，样例应该是过了的。

但纯贪心的思路是错误的，由于这道题的数据比较小，最多只有10，所以应当递归实现全排列枚举，然后判断是否存在一种排列能够使得所有飞机降落成功即可。

对于每一层递归，只需要知道上一层的降落结束时刻 \(last\)，由于每架飞机有一个最早降落时间 \(t\)，所以当前一层递归的最早降落结束时刻应取 \(max(last, t) + l\)，\(l\) 为降落所需时间。为了使得容错率更高，当最晚降落开始时间 \(t + d\) 大于等于 上一层的降落结束时刻，就可以将这架飞机作为下一个降落的飞机。

个人战况

我自己只想到贪心，估计只能过一半甚至都不到的样例。

代码

#include<iostream>
#include<cstring>
using namespace std;

const int N = 12;
int n;
struct node{
    int t, d, l;  //t为此飞机的最早降落时间 d为盘旋时间 l为降落所需时间
}p[N];
bool st[N];

//DFS求全排列模型
bool dfs(int u, int last){
    if(u == n) return true;

    for(int i = 0; i < n; i ++ ){
        int t = p[i].t, d = p[i].d, l = p[i].l;
        if(st[i]) continue;
        if(t + d >= last){  //最晚降落时间t+d大于等于上一层的降落结束时刻
            st[i] = true;
            if(dfs(u + 1, max(last, t) + l)) return true; //当前层的最早降落结束时刻为max(last,t)+l
            st[i] = false;
        }
    }

    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    int T; cin >> T;
    while(T -- ){
        cin >> n;
        for(int i = 0; i < n; i ++ ){
            int t, d, l; cin >> t >> d >> l;
            p[i] = {t, d, l};
        }

        memset(st, 0, sizeof(st));
        cout << (dfs(0, 0) ? "YES" : "NO") << endl;
    }

    return 0;
}

---

E：接龙数列 线性DP(最长上升子序列)

解题思路

逆向思维来考虑这道题，删除最少的数字得到接龙数列，实际上就是求整个序列的最长接龙子序列，而这个问题和最长上升子序列本质是一样的，不同的是，两个数字前后连接的方式不一样。如果说最长上升子序列前后数字的连接方式是前一个数字比后一个数字小，那么接龙数列前后数字的连接方式就是前一个数字的末尾位与后一个数字的首位相同，这本质上都是一样的，只是连接方式不同而已。

想到最长上升子序列还不足以做出这道题，因为数据范围达到了\(10^{5}\)，所以需要优化成一维线性DP。

可以发现，每一位数字的范围是 \(0 - 9\) ，只需要记录以每一位数字结尾的最长接龙数列长度即可，这样显然可以省去原本最长上升子序列内层的循环。

用 \(dp[i]\) 表示以数字 \(i\) 为末尾的最长接龙数列长度。对于每个数字，若其首位为 \(a\)，末位为 \(b\)，这个数字只有可能作为之前某个末位数字为 \(a\) 的数字后面，由此可得状态转移方程: \(dp[b] = max(dp[b], dp[a] + 1)\)

统计以每一位数字结尾的最长接龙数列长度的最大值，最后用原始序列长度减去这个最大值即答案。

个人战况

考试的时候只想到最长上升子序列，并没有想到优化方法，估计过了不到一半的样例。

代码

#include<iostream>
using namespace std;

int dp[10];   //dp[i]表示以数字i为末尾的最长接龙数列
int n, res;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n;
    for(int i = 1; i <= n; i ++ ){
        string s; cin >> s;
        int a = s[0] - '0', b = s.back() - '0';
        dp[b] = max(dp[b], dp[a] + 1);
        res = max(res, dp[b]);
    }

    cout << n - res << endl;

    return 0;
}

---

F：岛屿个数 BFS

解题思路

这道题比较考验思维能力。我一开始一直将思维卡死在如何判断一个岛屿连通块是否处于一个环内，也就是子岛屿的判断上，实际上，并不需要纠结于如何判断子岛屿。

很容易想到要使用 \(BFS\)，主要问题在于如何避免统计子岛屿。

只需要在外层加一层海洋，外层海洋可以涌入的地方，如果涌入的地方周围有陆地，那么这块陆地一定不在一个子岛屿中，反之，某个地方外层海洋无法涌入，一定是被某个环状岛屿包围所导致的，即位于某个子岛屿中。外层海洋无法涌入的地方，无需遍历。

从 \((0, 0)\) 处进行外层海洋的\(BFS\)，由于岛屿是上下左右四个方向的，相较于其而言，外层海洋\(BFS\)时需要八个方向进行遍历。在进行外层海洋\(BFS\)时，如果遍历到周围存在陆地，那么说明这个陆地所在的岛屿连通块需要被统计，此时进行岛屿\(BFS\)。

总之，需要实现两个\(BFS\)，并且在外层海洋\(BFS\)中，嵌套调用岛屿\(BFS\)。

个人战况

这道题很惨烈，我个人觉得自己做的 \(BFS\) 的题还是比较多的，对 \(BFS\) 类型的题比较有信心，但是这个题难住我了，考试的时候想了一会没有思路，最后直接写了个普通的 \(BFS\) 寄希望于骗分。

应该是0分，考完蓝桥杯省赛出来，因为这道题没能做出一点东西，感到挺难受的。

代码

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;

typedef pair<int, int> pii;
#define x first
#define y second
int dx[8] = {1, -1, 0, 0, 1, -1, 1, -1};
int dy[8] = {0, 0, 1, -1, 1, -1, -1, 1};
const int N = 55;
char g[N][N];
bool vis[N][N];
int n, m, res;

//岛屿BFS
void bfs(int sx, int sy){
    queue<pii> q;
    q.push({sx, sy});
    vis[sx][sy] = true;

    while(!q.empty()){
        auto [x, y] = q.front();
        q.pop();

        for(int k = 0; k < 4; k ++ ){
            int nx = x + dx[k], ny = y + dy[k];
            if(nx < 1 || nx > n || ny < 1 || ny > m) continue;
            if(g[nx][ny] == '0' || vis[nx][ny]) continue;
            q.push({nx, ny}), vis[nx][ny] = true;
        }
    }
}

//外层海洋BFS
void bfs_sea(int sx, int sy){
    queue<pii> q;
    q.push({sx, sy});
    vis[sx][sy] = true;

    while(!q.empty()){
        auto [x, y] = q.front();
        q.pop();

        for(int k = 0; k < 8; k ++ ){
            int nx = x + dx[k], ny = y + dy[k];
            if(nx < 0 || nx > n + 1 || ny < 0 || ny > m + 1 || vis[nx][ny]) continue;
            if(g[nx][ny] == '1') bfs(nx, ny), res ++ ; //如果遇到外层海水领近的陆地
            else q.push({nx, ny}), vis[nx][ny] = true;
        }
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    int T; cin >> T;
    while(T -- ){
        cin >> n >> m;
        res = 0;
        memset(g, '0', sizeof(g));
        memset(vis, 0, sizeof(vis));
        for(int i = 1; i <= n; i ++ )
            for(int j = 1; j <= m; j ++ )
                cin >> g[i][j];

        bfs_sea(0, 0);

        cout << res << endl;
    }

    return 0;
}

---

G：子串简写 前缀和

解题思路

题目大致意思就是给定一个字符串，统计长度大于等于 \(k\) ，且首尾字符分别为 \(c_{1}\) 和 \(c_{2}\) 的子字符串个数。

很明显可以用前缀和来求解。统计字符 \(c_{1}\) 的前缀和，可以由如下递推式得到前缀和:

\( \begin{cases} pre[i] = pre[i-1] + 1, & s[i]=c_{1} \\ pre[i] = pre[i-1], & s[i] \ne c_{1} \end{cases} \)

然后枚举字符 \(c_{2}\) 的位置，只要在原字符串上在遍历一次，累加 \((0, i-k+1]\) 范围内的前缀和：

\( \begin{cases} res = res + pre[i - k + 1], & s[i]=c_{2} \\ res = res, & s[i] \ne c_{2} \end{cases} \)

记得开 \(long long\) 。

个人战况

这道题基本上五分钟就做出来了，一下子就想到前缀和，应该是拿的全分。

代码

#include<iostream>
#include<cstring>
using namespace std;

typedef long long ll;
const int N = 5e5 + 10;
int pre[N], k;
char s[N], a, b;

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> k;
	cin >> s + 1 >> a >> b;

	int n = strlen(s + 1);
	//计算字符1的前缀和
	for(int i = 1; i <= n; i ++ )
		if(s[i] == a) pre[i] = pre[i - 1] + 1;
		else pre[i] = pre[i - 1];

	ll res = 0;
	//枚举字符2的位置 累加前缀和
	for(int i = k; i <= n; i ++ )
		if(s[i] == b) res += (ll)pre[i - k + 1];

	cout << res << endl;

	return 0;
}

---

H：整数删除 堆 + 双链表模拟

解题思路

题目大致意思就是，给定一个长度为 \(n\) 的序列，执行 \(k\) 次操作，操作为：找到当前序列中最小的数，删除它并将其累加到相邻的两个数中。最后得到 \(n - k\) 个数字，按照原始的相对顺序输出这些数字。

每次要取出最小数字，可以用小根堆进行模拟，存储序列的值及其下标，关键之处在于每次执行完删除操作后，数字相邻的下标位置会发生改变。

可以用双链表的方式存储相邻位置的下标，前驱数组为 \(l[i]\) ，记录的是下标 \(i\) 相邻的左边的下标；后继数组为 \(r[i]\)，记录的是下标 \(i\) 相邻的右边的下标。
所以删除操作即：\(l[r[i]] = l[i], r[l[i]] = r[i];\) ，\(i\) 为当前位置的下标。

采用了堆的数据结构，无法在删除数字的同时，直接将这个删除的数字累加到相邻位置的数字当中。所以，可以开一个数组 \(c[]\) 将累加值预先存起来，如果当前取出的最小值，累加值不是0，那么说明这个数字不应当作为当前的删除数字，此时需要加上\(c[i]\)，重新入队，并且将 \(c[i]\) 置0。

模拟直到最后堆中剩余 \(n - k\) 个数字，执行完最后一步操作后，堆中的有些数字依然存在累加值，并且需要按照原始的相对顺序输出，所以最后要累加到 \(res[]\) 数组中。

个人战况

这道题也挺惨的，考试的时候，模拟了半天，结果发现思路不对，没有想到用双链表的方式去记录相邻下标位置。消耗了很多时间，最后兜兜转转还是写了个暴力。

代码

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<iostream>
#include<queue>
#include<vector>
#include<functional>
using namespace std;

typedef long long ll;
typedef pair<ll, int> pii;
const int N = 5e5 + 10;
ll c[N], res[N];   //c[i]表示i处当前累加的和
int l[N], r[N];    //l[i]表示i的前驱下标  r[i]表示i的后一个下标
int n, k;

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n >> k;
	priority_queue<pii, vector<pii>, greater<pii> > q;  //小根堆
	for(int i = 1; i <= n; i ++ ){
		ll x; cin >> x;
		q.push({x, i});
		l[i] = i - 1, r[i] = i + 1;  //记录左右相邻的下标
	}

	while((int)q.size() > n - k){
		auto [cur, idx] = q.top();
		q.pop();

		if(c[idx]) q.push({cur + c[idx], idx}), c[idx] = 0; //如果c[idx]不为0，当前最小值不能弹出，累加后入队
		else{    //否则 当前最小值可以最为被选择的数
			c[l[idx]] += cur, c[r[idx]] += cur;      //左右下标累加值增加
			l[r[idx]] = l[idx], r[l[idx]] = r[idx];  //左右相邻下标更改
		}
	}

	while(!q.empty()){
		auto [cur, idx] = q.top();
		q.pop();
		res[idx] = cur + c[idx];
	}
	for(int i = 1; i <= n; i ++ ) 
		if(res[i]) cout << res[i] << ' ';

	return 0;
}

---

I：景区导游 最近公共祖先 tarjan求LCA

解题思路

题目大致意思就是给定一个树的结构，有 \(n - 1\) 条无向边，并且给了一个长度为 \(k\) 的序列，这个序列是访问节点的顺序。现在可以跳过这个序列中的一个节点，分别求出跳过第 \(1、2、3...k\) 节点的最短路径距离。

也就是说，需要求无向图两点之间的最短距离，可以通过求每两个点的最近公共祖先，进而求出两点间的最短距离。由于是无向图且是树的结构，树中的任何一个点都可以作为根节点，一般将节点 \(1\) 设为根节点。

假设此时需要求出节点 \(a\) 和节点 \(b\) 之间的最短距离，\(dist[a]\) 表示节点 \(a\) 到根节点的距离，\(dist[b]\) 表示节点 \(b\) 到根节点的距离，\(lca(a, b)\) 表示两个节点的最近公共祖先，姑且先将其命名为 \(anc\) 。通过画图可以知道，两点之间的最短距离就是 \(dist[a] + dist[b] - 2 * dist[anc]\) 。

在下图中，比如要求节点 \(6\) 和节点 \(5\) 的最短距离，可以看出两节点的最近公共祖先是节点 \(3\)，所以最近距离为 \(dist[5] + dist[6] - 2 * dist[3]\)。

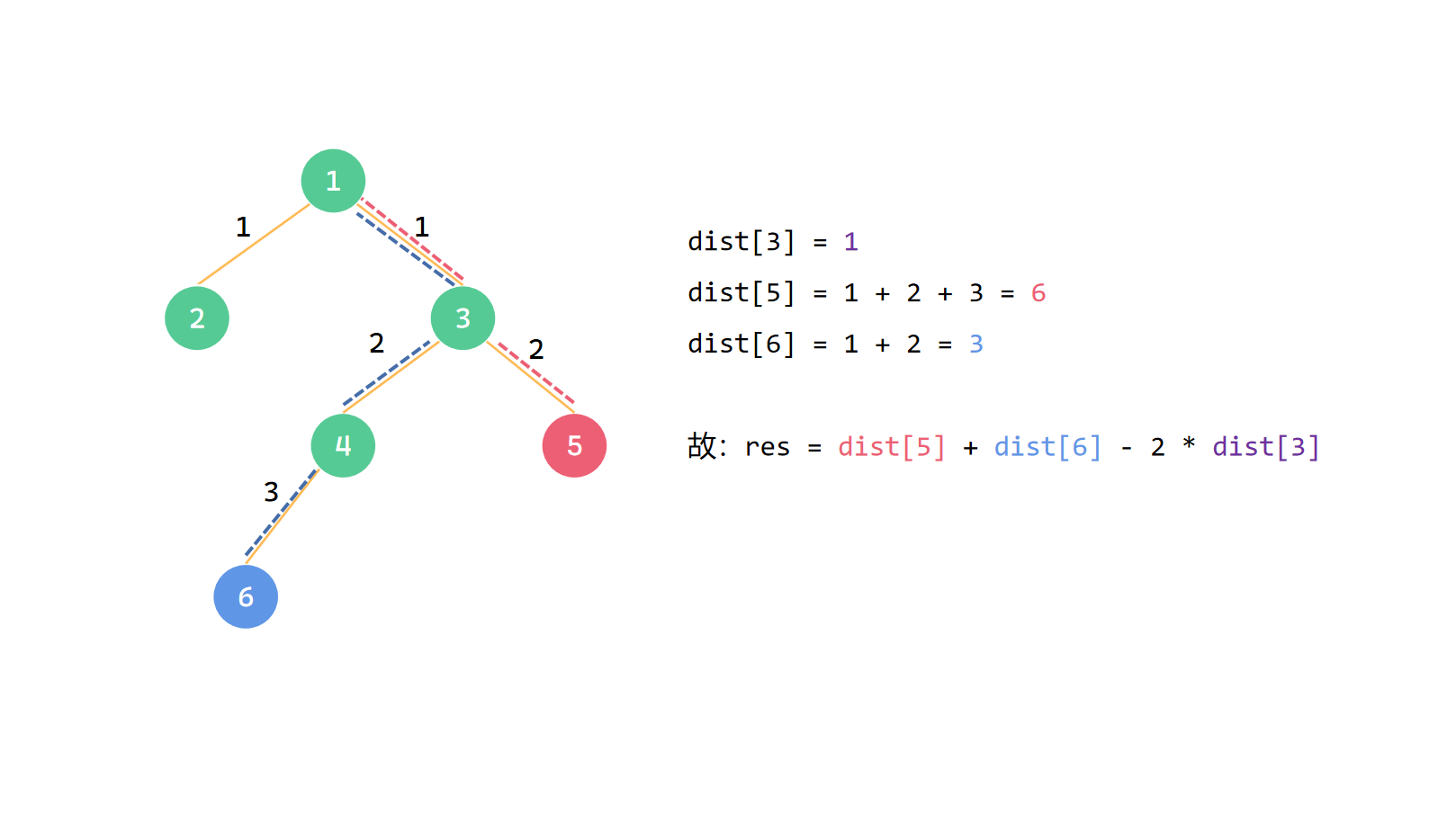
我自己用的是 \(tarjan\) 算法求 \(LCA\)。由题意可知，需要存储序列中相邻两个节点之间的询问，以及一个节点跳过其序列中右边相邻的节点，与右边相邻节点的下一个节点之间的询问。

然后先求出不跳过任何节点时的初始最短距离之和 \(sum\)，最后枚举中间跳过的节点，求出所有最短路径距离之和即可。假设跳过的节点为 \(i\)，那么需要减去节点 \(i\) 到 节点 \(i - 1\) 和 节点 \(i\) 到节点 \(i + 1\) 的最短路径距离，再加上节点 \(i - 1\) 到节点 \(i + 1\) 的最短路径。其中，跳过节点 \(1\) 和节点 \(k\) 需要特殊处理一下。

个人战况

这道题有点懊悔，自己 \(tarjan\) 求 \(LCA\) 的模板没有背熟，考试的时候应该是写错了，而且这道题也可以用倍增法求\(LCA\)，然而我之前几乎没有写过倍增。主要问题还有存储询问的方式，感觉自己的思维还是太死了，考试时没有想到用 \(map\) 来存储询问以及相对应的 \(LCA\) 。

代码

#include<iostream>
#include<cstring>
#include<map>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define x first
#define y second
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], w[M], idx;
map<int, int> query[N];
int fa[N];
int a[N];
ll dist[N];
bool st[N];
int n, k;

void init(){
	memset(h, -1, sizeof(h));
	for(int i = 1; i <= n; i ++ ) fa[i] = i;
}

int find(int x){
	return fa[x] == x ? x : (fa[x] = find(fa[x]));
}

void add(int a, int b, int c){
	e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}

//dfs求得根节点到节点距离
void dfs(int u, int fa){
	for(int i = h[u]; ~i; i = ne[i]){
		int v = e[i], c = w[i];
		if(fa == v) continue;
		dist[v] = dist[u] + c;
		dfs(v, u);
	}
}

//tarjan离线求LCA
void tarjan(int u){
	st[u] = true;
	for(int i = h[u]; ~i; i = ne[i]){
		int v = e[i];
		if(!st[v]){
			tarjan(v);
			fa[v] = u;
		}
	}

	for(auto p : query[u]){
		int v = p.x;
		if(st[v]) query[u][v] = find(v);
	}
}

//最近公共祖先
int lca(int a, int b){
	if(query[a][b]) return query[a][b];
	return query[b][a];
}

//两点最近距离
ll d1(int i){
	return dist[a[i]] + dist[a[i + 1]] - 2 * dist[lca(a[i], a[i + 1])];
}

//跳过i的两点最近距离
ll d2(int i){
	return dist[a[i - 1]] + dist[a[i + 1]] - 2 * dist[lca(a[i - 1], a[i + 1])];
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n >> k;
	init();
	for(int i = 0; i < n - 1; i ++ ){
		int u, v, c; cin >> u >> v >> c;
		add(u, v, c), add(v, u, c);
	}

	for(int i = 1; i <= k; i ++ ) cin >> a[i];
	for(int i = 1; i <= k - 1; i ++ ) query[a[i]][a[i + 1]] = 0, query[a[i + 1]][a[i]] = 0;
	for(int i = 1; i <= k - 2; i ++ ) query[a[i]][a[i + 2]] = 0, query[a[i + 2]][a[i]] = 0;

	dfs(1, -1);
	tarjan(1);

	ll sum = 0;
	for(int i = 1; i <= k - 1; i ++ ) sum += d1(i);  //原始路线距离

	//枚举跳过的节点
	cout << sum - d1(1) << ' ';      //跳过节点1
	for(int i = 2; i <= k - 1; i ++ ) cout << sum - d1(i - 1) - d1(i) + d2(i) << ' ';
	cout << sum - d1(k - 1) << endl; //跳过节点k	

	return 0;
}

---

J：砍树 树上差分 + tarjan求LCA

解题思路

题目大致意思就是，给定一个树的结构，树有 \(n\) 个节点，给定 \(m\) 对节点，找到一个编号最大的边，使得去除这条边之后，每一对节点不连通。

由于这是一个树的结构，节点与节点之间的路径是唯一的。所以，假设每一对节点之间的路径都走一遍，在 \(m\) 对节点所构成的路径网络中，有一条边经过了 \(m\) 次，那么这条边就是每一对节点之间路径上都存在的边。故去除这条边之后，能够使得每对节点不连通。树中可能存在多条边满足这个条件，所以需要预先记录边的编号，并且最后返回编号最大的边。

对于每条边经过的次数，采用树上差分（边差分）来处理。

边差分公式：

\( \begin{cases} diff[a] = diff[a] + 1 \\ diff[b] = diff[b] + 1 \\ diff[lca(a, b)] = diff[lca(a,b)] - 2 \end{cases} \)

可以根据一维差分公式对其进行推导，这里不多赘述。

然后用 \(dfs\) 在树上自底向上再求一下前缀和就可以了。在 \(dfs\) 过程中，如果存在经过了 \(m\) 次的边且编号比先前更大，则进行答案的更新。

个人战况

看到这道题的时候以及没时间了，一点代码也没写。不过即使有时间这题也做不出，之前没有学习过树上差分，我要学的东西还是很多啊......

代码

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], id[M], idx;
int fa[N];
int st[N];
int diff[N];
vector<int> query[N];
int n, m, res;

void init(){
	memset(h, -1, sizeof(h));
	for(int i = 1; i <= n; i ++ ) fa[i] = i;
}

void add(int a, int b, int i){
	e[idx] = b, ne[idx] = h[a], id[idx] = i, h[a] = idx ++ ; 
}

int find(int x){
	return fa[x] == x ? x : (fa[x] = find(fa[x]));
}

void tarjan(int u){
    st[u] = 1;
    for(int i=h[u]; ~i; i = ne[i]){
        int v = e[i];
        if(st[v])continue;
        tarjan(v);
        fa[v] = u;
    }

    for(auto v : query[u])
        if(st[v] == 2) diff[v] ++ , diff[u] ++ , diff[find(v)] -= 2;
    st[u] = 2;
}

int dfs(int u, int fa){
	int sum = diff[u];
	for(int i = h[u]; ~i; i = ne[i]){
		int v = e[i];
		if(v == fa) continue;
		int c = dfs(v, u);
		if(c == m) res = max(res, id[i]);
		sum += c;
	}
	return sum;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n >> m;
	init();
	for(int i = 1; i <= n - 1; i ++ ){
		int u, v; cin >> u >> v;
		add(u, v, i), add(v, u, i);
	}

	for(int i = 0; i < m; i ++ ){
		int u, v; cin >> u >> v;
		query[u].push_back(v), query[v].push_back(u);
	}

	tarjan(1);
	dfs(1, -1);

	cout << (res ? res : -1) << endl;

	return 0;
}

---

个人总结

在写题解的过程中，我时刻在反思自己有些方法为什么当时没有想到，以及我究竟能够在有限的时间里解决多少问题。我并没有在短短的四小时内将自己的实力发挥到极致，不过把自己所会的东西都做好，还是非常不容易的，很明显我没有做到这一点，这也是我自己能力不足、缺乏经验所导致的。未来的比赛有很多，虽然这次蓝桥杯拿到了省一，但是我并不觉得我证明了自己的实力有多强，事实上，我只是发挥得马马虎虎并且运气还不错而已。

我所在的学校在算法竞赛这一方面很弱，这是难以忽略的事实。也许在学校里我个人还算是不错的，但是看到别的学校，算法竞赛氛围真的很好，努力的学生很多，高手很多，而且老师也都很用心。我很羡慕。

我一直以来都想去到更高的平台参加比赛，去参加ACM什么的。我身处的环境，基本上决定了我未来的道路会充满挫折，但这不会阻挡我去飞向更高的天空。