「学习笔记」略谈点分治
点分治适合处理大规模的树上路径信息问题。
引入
给定一棵 \(n\) 个点树和一个整数 \(k\),求树上两点间的距离小于等于 \(k\) 的点对有多少。
对于这个题,如果我们进行 \(O_{n^3}\) 搜索,那只要 \(n\) 一大,铁定超时。
所以,我们要用一个更优秀的解法,这就是我们的点分治。
淀粉质可好吃了
变量
typedef pair<int, int> pii;
const int N = 4e4 + 10;
int n, k, rt, ans, sum;
int siz[N], maxp[N], dis[N], ok[N];
bool vis[N];
vector<pii> son[N];
n: 点数;
k: 限定距离;
rt: 根节点;
sum: 总结点数(找重心要用到);
siz: 子树大小;
maxp: 最大的子树的大小;
dis: 每个节点到根节点的距离;
ok: 栈;
vis: 标记;
son: 存图。
过程
1. 找重心
为什么是找重心?
其所有的子树中最大的子树节点数最少,在所有点中,重心是最优的选择。
找到重心后,以重心为根开始操作。
void get_root(int u, int fat) {
siz[u] = 1;
maxp[u] = 0;
for (pii it : son[u]) {
int v = it.first;
if (v == fat || vis[v]) continue;
get_root(v, u);
siz[u] += siz[v];
maxp[u] = max(maxp[u], siz[v]);
}
maxp[u] = max(maxp[u], sum - siz[u]);
if (maxp[u] < maxp[rt]) rt = u;
}
这里并不是很难。
2. 处理答案
对于每个根节点,我们进行搜索,会得到每个节点到根节点的距离。
我们现在要求出经过根节点的距离小于等于 \(k\) 的点对个数。
我们将所有点的距离从小到大排一个序,设置左右两个指针,如果左指针和右指针所指向的节点到根节点的距离小于等于 \(k\),则两个指针之间所有的节点到左指针所指向的节点的距离都小于等于 \(k\),与此同时 l ++,如果左右指针所指向的节点的距离之和大于 \(k\),那么右指针就要左移,即 -- r。
然后我们对每个节点都这样搜一遍,将答案加出来,就可以轻松加愉快的切掉这个问题了
吗?
考虑一下,如果是下面这种情况
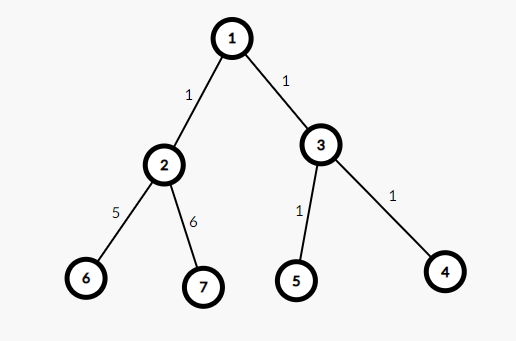
假设 \(k = 5\),那么以 \(1\) 为根节点时,\(4\) 与 \(5\) 很显然是符合的,我们将它加入答案。
然后,当我们又以 \(3\) 为根节点时,\(4\) 和 \(5\) 这个点对我们就又统计了一次。
有什么问题?重复啦!
原因也很简单,因为 \(4\) 和 \(5\) 在同一个子树内,因此只要它们在这个大的树内符合要求,那么它们在它们的小子树内也一定符合要求,那么就一定会有重复,因此,利用容斥的原理,我们先求出总的答案,然后再减去重复的部分。
如何检验重复的部分呢?
我们发现它们共同经过了一条边 \(1 - 3\),所以我们再次搜索,这次直接初始化 dis[3] = 1,然后其他的依旧按照操作,最后如果他们的距离小于等于 \(k\),则这就是重复的部分,统计一下,最后减去即可。
减去之后,就在子树里找重心,设置新的根节点,开始新的答案统计,与此同时,我们要将原来的根节点打上标记,防止搜索范围离开了这个子树。
(或许这就是点“分治”的所在,搜完一个重心后,相当于把这个重心删除,然后就将一颗树分成多个互相之间没有联系的小子树,各自进行搜索)
int calc(int u, int val) {
ok[0] = 0;
dis[u] = val;
dfs(u, 0);
sort(ok + 1, ok + ok[0] + 1);
int cnt = 0, l = 1, r = ok[0];
while (l < r) {
if (ok[l] + ok[r] <= k) {
cnt += (r - l ++);
}
else {
r --;
}
}
return cnt;
}
void work(int u) {
ans += calc(u, 0);
vis[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (vis[v]) continue;
ans -= calc(v, w);
maxp[rt = 0] = sum = siz[v];
get_root(v, 0);
work(rt);
}
}
关于 sum = siz[v];,当我们再次找重心时,是要在这个子树中找重心,不能超出这个子树,因此要将总个数也设为 siz[v]。
3. 处理到根节点的距离
这个,应该就没什么好说的了。
void dfs(int u, int fat) {
ok[++ ok[0]] = dis[u];
siz[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (v == fat || vis[v]) continue;
dis[v] = dis[u] + w;
dfs(v, u);
siz[u] += siz[v];
}
}
看到这,你已经看完了点分治的核心步骤,让我们把代码整合一下,去切掉这道模板题 Tree。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 4e4 + 10;
int n, k, rt, ans, sum;
int siz[N], maxp[N], dis[N], ok[N];
bool vis[N];
vector<pii> son[N];
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
void get_root(int u, int fat) {
siz[u] = 1;
maxp[u] = 0;
for (pii it : son[u]) {
int v = it.first;
if (v == fat || vis[v]) continue;
get_root(v, u);
siz[u] += siz[v];
maxp[u] = max(maxp[u], siz[v]);
}
maxp[u] = max(maxp[u], sum - siz[u]);
if (maxp[u] < maxp[rt]) rt = u;
}
void dfs(int u, int fat) {
ok[++ ok[0]] = dis[u];
siz[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (v == fat || vis[v]) continue;
dis[v] = dis[u] + w;
dfs(v, u);
siz[u] += siz[v];
}
}
int calc(int u, int val) {
ok[0] = 0;
dis[u] = val;
dfs(u, 0);
sort(ok + 1, ok + ok[0] + 1);
int cnt = 0, l = 1, r = ok[0];
while (l < r) {
if (ok[l] + ok[r] <= k) {
cnt += (r - l ++);
}
else {
r --;
}
}
return cnt;
}
void work(int u) {
ans += calc(u, 0);
vis[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (vis[v]) continue;
ans -= calc(v, w);
maxp[rt = 0] = sum = siz[v];
get_root(v, 0);
work(rt);
}
}
int main() {
n = read();
for (int i = 1, u, v, w; i < n; ++ i) {
u = read(), v = read(), w = read();
son[u].push_back({v, w});
son[v].push_back({u, w});
}
k = read();
maxp[rt = 0] = sum = n;
get_root(1, 0);
work(rt);
printf("%d\n", ans);
return 0;
}
其他题目
模板题(大雾)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, ll> pil;
const int N = 1e4 + 5;
int n, m, sum, rt;
int q[N], siz[N], maxs[N], can[N], dis[N];
int tp[N];
bool ok[N], vis[N];
vector<pil> son[N];
bool cmp(int x, int y) {
return dis[x] < dis[y];
}
void get_root(int u, int fat, int tot) {
siz[u] = 1;
maxs[u] = 0;
for (auto [v, w] : son[u]) {
if (v == fat || vis[v]) continue;
get_root(v, u, tot);
siz[u] += siz[v];
maxs[u] = max(siz[v], maxs[u]);
}
maxs[u] = max(maxs[u], tot - siz[u]);
if (!rt || maxs[u] < maxs[rt]) {
rt = u;
}
}
void dfs(int u, int fat, int d, int from) {
can[++ can[0]] = u;
dis[u] = d;
tp[u] = from;
for (auto [v, w] : son[u]) {
if (v == fat || vis[v]) continue;
dfs(v, u, d + w, from);
}
}
void calc(int u) {
can[0] = 0;
can[++ can[0]] = u;
dis[u] = 0;
tp[u] = u;
for (auto [v, w] : son[u]) {
if (vis[v]) continue;
dfs(v, u, w, v);
}
sort(can + 1, can + can[0] + 1, cmp);
for (int i = 1; i <= m; ++ i) {
int l = 1, r = can[0];
if (ok[i]) continue;
while (l < r) {
if (dis[can[l]] + dis[can[r]] > q[i]) {
r --;
}
else if (dis[can[l]] + dis[can[r]] < q[i]) {
++ l;
}
else if (tp[can[l]] == tp[can[r]]) {
if (dis[can[r]] == dis[can[r - 1]]) {
-- r;
}
else ++ l;
}
else {
ok[i] = true;
break;
}
}
}
}
void work(int u) {
vis[u] = true;
calc(u);
for (auto [v, w] : son[u]) {
if (vis[v]) continue;
rt = 0;
get_root(v, 0, siz[v]);
work(rt);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1, x, y, z; i < n; ++ i) {
cin >> x >> y >> z;
son[x].push_back({y, z});
son[y].push_back({x, z});
}
for (int i = 1; i <= m; ++ i) {
cin >> q[i];
if (!q[i]) ok[i] = 1;
}
maxs[0] = n;
get_root(1, 0, n);
work(rt);
for (int i = 1; i <= m; ++ i) {
if (ok[i]) {
cout << "AYE" << '\n';
}
else {
cout << "NAY" << '\n';
}
}
return 0;
}
