「学习笔记」平衡树——splay 一
Splay,一种平衡树,同时也是二叉排序树,与 Treap 不同,它不需要维护堆的性质,它由 Daniel Sleator 和 Robert Tarjan(没错,tarjan,又是他)创造,伸展树是一种自调整二叉树,它会将一个节点沿着到根的路径旋转上去。
空间效率:\(O_n\)
摊平时间效率:\(O_{logn}\)
建议先学会 Treap。
存储结构
int ch[N][2],fa[N];//左孩子,右孩子,父亲
ll val[N],siz[N],cnt[N];//点值
数组存储,也可以用结构体。
基本操作
一、旋转
与 treap 的旋转无太大差异,只要注意更新父节点就行了,记得要更新 \(siz\)。
Splay 的旋转函数的参数,是转上去的那个数值,这里与 Treap 不同,Treap 是转下来的数值。
这里旋转一定要注意次序,明白先处理哪个,再处理哪个,否则会 RE!
一定要先处理 \(x\) 与 \(y\) 的孩子,再处理 \(x\) 与 \(y\)。
void pushup(int id)//更新siz
{
siz[id]=siz[ch[id][0]]+siz[ch[id][1]]+cnt[id];
}
void spin(int x)
{
rint y=fa[x],z=fa[y],d=(ch[y][1]==x);//d 判断x是y的左孩子还是右孩子
ch[z][ch[z][1]==y]=x,fa[x]=z;//处理x与z的关系
ch[y][d]=ch[x][d^1],fa[ch[x][d^1]]=y;//处理y的孩子与x的孩子的关系
ch[x][d^1]=y;fa[y]=x;//处理y与x的关系
pushup(y);//先更新y
pushup(x);//在更新x
}
二、伸展
情况一
\(x\) 要移动到父节点的位置。

自己懒得画了,图扒的教练的
直接旋转 \(x\) 即可。
情况二
\(x\) 点要移到到 \(g\) 或更向上的位置且 \(g\) -> \(p\) 和 \(p\) -> \(x\) 是同一方向。
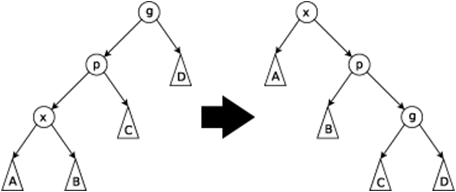
这里要先旋转 \(p\),再旋转 \(x\)。
情况三
\(x\) 点要移到到 \(g\) 或更向上的位置且 \(g\) -> \(p\) 和 \(p\) -> \(x\) 不是是同一方向。
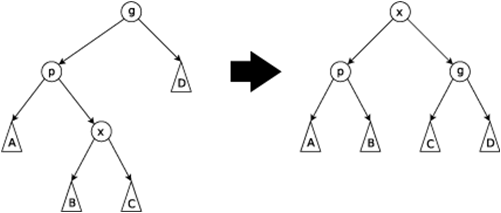
这里旋转两次 \(x\)。
其实,到这里你会发现,最后一次都是旋转 \(x\)。
void splay(int x,int goal)
{
while(fa[x]!=goal)//判断是否已经到目标点的下边
{
rint y=fa[x],z=fa[y];
if(z!=goal)//判断是情况一还是情况二、三
(ch[y][0]==x)^(ch[z][0]==y)?spin(x):spin(y);
//判断是情况二还是情况三
spin(x);
}
if(goal==0) root=x;//如果移动到了根节点,则更新根节点
}
三、插入节点
只要记得处理父节点就行了。
void insert(ll x)
{
int u=root,fat=0;
while(u&&val[u]!=x)//先向下找
{
fat=u;
u=ch[u][x>val[u]];
}
if(u) cnt[u]++;
else
{
u=++tot;
if(fat) ch[fat][x>val[fat]]=u;//如果不是根节点,更新孩子节点
fa[u]=fat;//插入操作
val[u]=x;
siz[u]=1;
cnt[u]=1;
}
splay(u,0);//每次都要伸展,避免成链
}
四、查找结点
按照二叉排序树找到节点,然后将该节点伸展到到根节点就行了。
void find(ll x)
{
int u=root;
if(!u) return;//不存在该节点,直接返回
while(ch[u][x>val[u]]&&x!=val[u])//找到该节点的位置
u=ch[u][x>val[u]];
splay(u,0);//伸展
}
五、查找前驱后继
先将要查找的值的位置或相邻的位置伸展到根节点,然后在左右子树中搜索。
int get(ll x,int d)//d:0找前驱 1找后继
{
find(x);//先伸展
int u=root;
if((val[u]>x&&d)||(val[u]<x&&!d)) return u;
//如果该节点已经符合要求,直接返回位置
u=ch[u][d];//找到左右子树
while(ch[u][d^1]) u=ch[u][d^1];
//找左子树中最大的或右子树中最小的(关键看你找前驱还是后继)
return u;//返回前驱或后继的位置
}
六、删除节点
先找到前驱和后继,将前驱伸展到根节点,将后继伸展到前驱下面,根据二叉查找树的性质,后继的左孩子就是我们要删的点,进行操作即可。
void del(ll x)
{
int pre=get(x,0),nxt=get(x,1);//找前驱后继
splay(pre,0),splay(nxt,pre);//伸展
int id=ch[nxt][0];//要删除的点
if(cnt[id]>1)//如果这个数值有重复,直接--cnt即可
{
--cnt[id];
splay(id,0);//伸展
}
else
{
ch[nxt][0]=0,fa[id]=0;//先切断联系
val[id]=0,cnt[id]=0,siz[id]=0;//再进行删除
pushup(nxt),pushup(pre);//最后更新siz
}
}
