【LeetCode专题#基本计算器】基本计算器I，图解中序表达式转逆波兰表达式，太难了

基本计算器

https://leetcode.cn/problems/basic-calculator/?envType=list&envId=cKNEfNsF

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "1 + 1"
输出：2

示例 2：

输入：s = " 2-1 + 2 "
输出：3

示例 3：

输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

提示：

1 <= s.length <= 3 * 105
s 由数字、'+'、'-'、'('、')'、和 ' ' 组成
s 表示一个有效的表达式
'+' 不能用作一元运算(例如， "+1" 和 "+(2 + 3)" 无效)
'-' 可以用作一元运算(即 "-1" 和 "-(2 + 3)" 是有效的)
输入中不存在两个连续的操作符
每个数字和运行的计算将适合于一个有符号的 32位 整数

思路

本题由两种方法解决，一种是单调栈，另一种是逆波兰表达式（主要考虑逆波兰）

使用逆波兰表达式的话大概思路如下：

创建一个操作符栈op和一个结果栈res并将字符串s（s为中序表达式）的第一个字符设置为当前字符

先将输入的中序字符串s中的空格处理掉，然后按以下规则从左到右依次遍历中序字符串s的每个字符

? a. 如果当前字符是数字，则直接压入结果栈中；

? b. 如果当前字符是操作符，则分情况讨论：

? i. 如果当前操作符优先级低于或等于操作符栈顶元素，则将操作符栈顶元素弹出并加入结果栈中，重复此步骤直到操作符栈为空或 者操作符的优先级高于栈顶元素为止。然后将操作符压入操作符栈中。

? ii. 如果当前操作符优先级高于操作符栈顶元素，则直接将操作符压入操作符栈中。

? c. 如果当前字符是左括号，则将其压入操作符栈中。

? d. 如果当前字符是右括号，则不断地将操作符栈顶元素弹出并加入结果栈中，直到遇到左括号为止。

当中序表达式遍历完毕后，如果操作符栈中还有剩余元素，则将其全部弹出并加入结果栈中。 最后，结果栈中的元素就是逆波兰表达式。

假设我们有中序表达式 "3 + 4 * (2 - 1)"，现在来演示如何将其转换为逆波兰表达式：

首先先去空格，得到"3+4*(2-1)"
然后，创建操作符栈和结果栈，并将表达式的第一个字符 "3" 设置为当前字符。
接着，遍历表达式中的下一个字符 "+":
	因为 "+" 是一个操作符，所以将其与操作符栈顶元素比较。此时操作符栈为空，因此直接将 "+" 压入操作符栈中。

下一个字符是数字 "4"，因此将其直接压入结果栈中。

下一个字符是操作符 "*"，再次将其与操作符栈顶元素比较。因为 "*" 的优先级高于 "+"，所以直接将 "*" 压入操作符栈中。

下一个字符是左括号 "("，将其压入操作符栈中。

下一个字符是数字 "2"，将其压入结果栈中。

下一个字符是操作符 "-"，将其压入操作符栈中。

下一个字符是数字 "1"，将其压入结果栈中。

下一个字符是右括号 ")"，此时需要不断地将操作符栈顶元素弹出并加入结果栈中，直到遇到左括号为止。因此，弹出 "-"、"1" 和 "(" 并将它们依次加入结果栈中。

现在已经遍历完了全部字符，但是操作符栈中还有剩余元素"*"和"+"，因此将其弹出并加入结果栈中。

最后，结果栈中
的元素就是逆波兰表达式："3421-*+"

这个逆波兰表达式可以通过栈来求值。

图解如下：

遍历中序字符串s，将操作符按优先级压入操作符栈op，将数字按遍历顺序（从左到右）压入结果栈res

直到遇到右括号，这时，不断遍历操作符栈op，将操作符元素压入结果栈res

直到遇到左括号结束

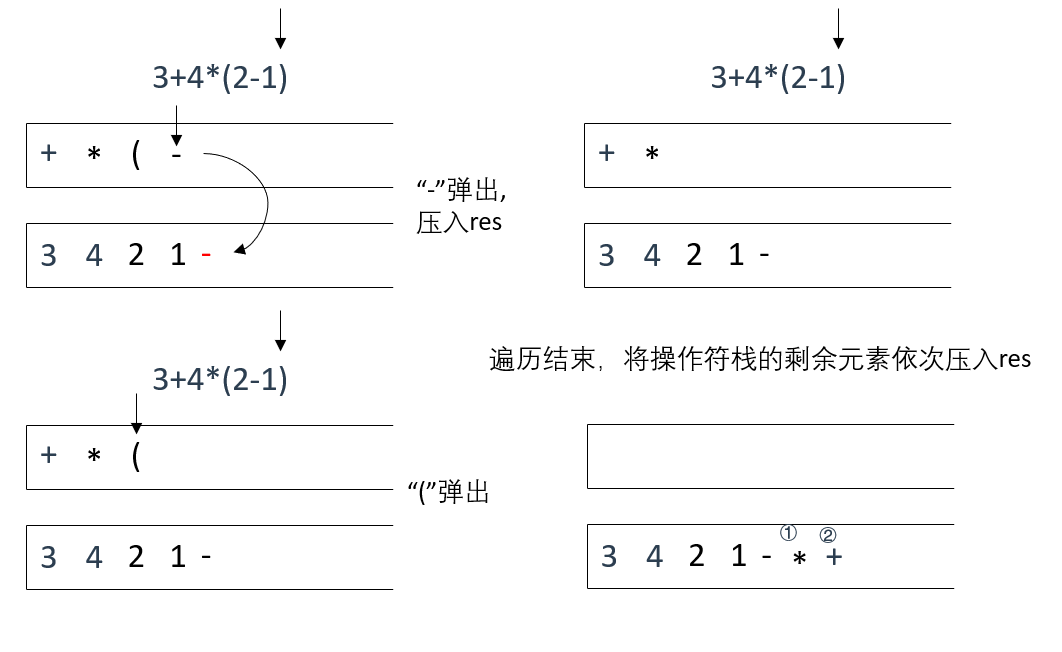
此时，如果op内还有剩余操作符元素，将其依次弹出并加入res

得到结果"3421-*+"

逆波兰表达式实现思路

代码实现中，我们需要写四个函数：去除空格的函数removeBlack、逆波兰表达式转换函数toRPN、逆波兰表达式求解函数getRes以及主函数calculate

class Solution {
private:
    //有一个移除空格的函数
    string removeBlack(string s){
        string res = "";
        for(char c : s){
            if(c != ' ') res += c;
        }
        return res;
    }

    //将表达式分割为后缀表达式
    void toRPN(string s){
        ...
    }
    
    //将表达式分割为后缀表达式
    void getRes(){
        ...
    }  

public:
    int calculate(string s) {

    }
};

getRes()函数再计算逆波兰表达式的结果时，需要一个vector作为输入

这里还添加了一个priority函数用于返回操作符的优先级

因此，toRPN的返回值应该是vector，我们按照上面对于逆波兰表达式的转换思路，编写toRPN如下

class Solution {
private:
    //有一个移除空格的函数
    string removeBlack(string s){
        string res = "";
        for(char c : s){
            if(c != ' ') res += c;
        }
        return res;
    }
    // 定义运算符优先级
    int priority(char op) {
        if (op == '+' || op == '-') return 1;
        if (op == '*' || op == '/') return 2;
        return 0;
    }
    //将中序表达式分割为后缀表达式
    vector<string> toRPN(string s){
        stack<string> op;//操作符栈
        vector<string> res;//结果栈
        string num = "";//记录多位数字
        for(char c : s){////遍历当前输入的中序字符串s,判断当前字符的类型
            if(isdigit(c)){//当前字符c为数字
                num += c;//为了防止当前数字有多位数，先用num收集
            }else if(is_operator(c)){//当前字符c为操作符
                if(!num.empty()){//证明num已经将数字收集完毕，压入结果栈
                    res.push_back(num);
                    num = "";
                }
                //处理操作符逻辑，压入op
                //当前op中有操作符元素，比较两者优先级
                //【如果op.top() == "("则说明现在之前遇到了")",现在正在弹出"("之前的所有操作符】 
                //以下情况表示栈顶运算符的优先级大于等于当前读入的运算符c的优先级
                while(!op.empty() && op.top() != "(" && priority(op.top()) >= priority(string(1, c))){
                    res.push_back(op.top());//将优先级高的先压入结果栈res
                    op.pop();//然后弹掉
                }
                op.push(string(1, c));//当前读入的运算符优先级大于等于栈顶运算符
            }else if(c == '('){//当前字符c为左括号
                if(!num.empty()){//证明num已经将数字收集完毕，压入结果栈
                    res.push_back(num);
                    num = "";
                }
                op.push("(");
            }else if(c == ')'){//当前字符c为右括号
                if(!num.empty()){//证明num已经将数字收集完毕，压入结果栈
                    res.push_back(num);
                    num = "";
                }
                while(op.top() != "(" && !op.empty()){//不断弹出操作符栈顶元素加入到结果栈res中
                    res.push_back(op.top());
                    op.pop();
                }
                op.pop();//多弹一次取出左括号
            }
        }//遍历处理完毕，如果num和操作符栈还有剩的元素，先将num压入res再压op
        if(!num.empty()){//如果还有数字未入结果栈，则加入
            res.push_back(num);
        }
        while(!op.empty()){//将剩余的操作符入结果栈
            res.push_back(op.top());
            op.pop();
        }
        return res;
    }
    
    //计算逆波兰表达式，LeetCode.150
    int getRes(vector<string>& tokens){
        
    }  

public:
    int calculate(string s) {

    }
};

第一版代码

基于LeetCode.150的知识补充完getRes函数后我们得到了第一版代码，是不是很爽？示例用例都ac

class Solution {
private:
    //有一个移除空格的函数 //只是将原字符串的空格去除后，生成了一个新的字符串，但并没有将原字符串进行修改,错误
    string removeBlack(string& s){
        string res = "";
        for(char c : s){
            if(c != ' ') res += c;
        }
        return res;
    }
    // 定义运算符优先级
    int priority(string op) {
        if (op == "+" || op == "-") return 1;
        if (op == "*" || op == "/") return 2;
        return 0;
    }

    bool is_operator(char c) {//判断当前元素是否为操作符
        switch(c) {
            case '+':
            case '-':
            case '*':
            case '/':
                return true;
            default:
                return false;
            }
    }
    
    //将中序表达式分割为后缀表达式
    vector<string> toRPN(string s){
        stack<string> op;//操作符栈
        vector<string> res;//结果栈
        string num = "";//记录多位数字
        for(char c : s){////遍历当前输入的中序字符串s,判断当前字符的类型
            if(isdigit(c)){//当前字符c为数字
                num += c;//为了防止当前数字有多位数，先用num收集
            }else if(is_operator(c)){//当前字符c为操作符
                if(!num.empty()){//证明num已经将数字收集完毕，压入结果栈
                    res.push_back(num);
                    num = "";
                }
                //处理操作符逻辑，压入op
                //当前op中有操作符元素，比较两者优先级
                //【如果op.top() == "("则说明现在之前遇到了")",现在正在弹出"("之前的所有操作符】 
                //以下情况表示栈顶运算符的优先级大于等于当前读入的运算符c的优先级
                while(!op.empty() && op.top() != "(" && priority(op.top()) >= priority(string(1, c))){
                    res.push_back(op.top());//将优先级高的先压入结果栈res
                    op.pop();//然后弹掉
                }
                op.push(string(1, c));//当前读入的运算符优先级大于等于栈顶运算符
            }else if(c == '('){//当前字符c为左括号
                if(!num.empty()){//证明num已经将数字收集完毕，压入结果栈
                    res.push_back(num);
                    num = "";
                }
                op.push("(");
            }else if(c == ')'){//当前字符c为右括号
                if(!num.empty()){//证明num已经将数字收集完毕，压入结果栈
                    res.push_back(num);
                    num = "";
                }
                while(op.top() != "(" && !op.empty()){//不断弹出操作符栈顶元素加入到结果栈res中
                    res.push_back(op.top());
                    op.pop();
                }
                op.pop();//多弹一次取出左括号
            }
        }//遍历处理完毕，如果num和操作符栈还有剩的元素，先将num压入res再压op
        if(!num.empty()){//如果还有数字未入结果栈，则加入
            res.push_back(num);
        }
        while(!op.empty()){//将剩余的操作符入结果栈
            res.push_back(op.top());
            op.pop();
        }
        return res;
    }
    
    //计算逆波兰表达式，LeetCode.150
    int getRes(vector<string>& tokens){
        stack<long long> st;
        //遍历字符串
        for(int i = 0; i < tokens.size(); ++i){
            if(tokens[i] == "+"|| tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){//遇到运算符
                //取两个数
                long long num1 = st.top();
                st.pop();
                long long num2 = st.top();
                st.pop();
                //判断运算符，做相应计算并压栈//注意计算顺序，num2[运算符]num1
                if(tokens[i] == "+") st.push(num2 + num1);
                if(tokens[i] == "-") st.push(num2 - num1);
                if(tokens[i] == "*") st.push(num2 * num1);
                if(tokens[i] == "/") st.push(num2 / num1);
            }else{//遇到数字
                //转为整型，压栈
                st.push(stoll(tokens[i]));
            }
        }
        int res = st.top();
        st.pop();//内存回收
        return res;
    }  

public:
    int calculate(string s) {
        string noBlackIn_s = removeBlack(s);
        vector<string> rpn4s = toRPN(noBlackIn_s);
        
        return getRes(rpn4s);
    }
};

坑

但是，上述代码在测试用例为"1-( -2)"时报错了（咬牙切齿）

Line 171: Char 16: runtime error: reference binding to misaligned address 0xbebebebebebec0b6 for type 'long long', which requires 8 byte alignment (stl_deque.h)
0xbebebebebebec0b6: note: pointer points here
<memory cannot be printed>
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior /usr/bin/../lib/gcc/x86_64-linux-gnu/9/../../../../include/c++/9/bits/stl_deque.h:180:16

原因大概是因为按照我们之前的逻辑写的toRPN函数没有考虑到有负数的情况。。。

怎么办，改呗

第二版代码

考虑了负号，但是测试用例仍然只通过24/44

class Solution {
private:
    string removeBlack(string& s){
        string res = "";
        int i = 0, n = s.size();
        while(i < n){
            if(s[i] == ' ') ++i;
            else if(s[i] == '-'){
                // 跳过空格
                while(i < n && s[i] == ' ') ++i;
                // 判断减号前是否有数字或左括号
                if(i == 0 || s[i-1] == '('){
                    res += '0';
                }
                // 将减号复制到新字符串中
                res += '-';
                ++i;
                // 将减号后面的数字复制到新字符串中
                while(i < n && isdigit(s[i])){
                    res += s[i];
                    ++i;
                }
                // 在数字后面添加空格，以便后续处理
                res += ' ';
            }else{
                // 复制其他字符到新字符串中
                res += s[i];
                ++i;
            }
        }
        return res;
    }
    int priority(string op) {
        if (op == "+" || op == "-") return 1;
        if (op == "*" || op == "/") return 2;
        return 0;
    }

    bool is_operator(char c) {
        switch(c) {
            case '+':
            case '-':
            case '*':
            case '/':
                return true;
            default:
                return false;
        }
    }


    vector<string> toRPN(string s){
        stack<string> op;
        vector<string> res;
        string num = "";
        for(int i = 0; i < s.size(); ++i){
            char c = s[i];
            if(isdigit(c)){
                num += c;
            }else if(is_operator(c)){
                if(!num.empty()){
                    res.push_back(num);
                    num = "";
                }
                while(!op.empty() && op.top() != "(" && priority(op.top()) >= priority(string(1, c))){
                    res.push_back(op.top());
                    op.pop();
                }
                op.push(string(1, c));
            }else if(c == '('){
                if(!num.empty()){
                    res.push_back(num);
                    num = "";
                }
                op.push("(");
            }else if(c == ')'){
                if(!num.empty()){
                    res.push_back(num);
                    num = "";
                }
                while(op.top() != "(" && !op.empty()){
                    res.push_back(op.top());
                    op.pop();
                }
                op.pop();
            }else if(c == ' '){ // 处理空格
                if(!num.empty()){
                    res.push_back(num);
                    num = "";
                }
                // 如果前一个字符不是减号，则将空格添加到新字符串中
                if(i > 0 && s[i-1] != '-'){
                    res.push_back(" ");
                }
            }
        }
        if(!num.empty()){
            res.push_back(num);
        }
        while(!op.empty()){
            res.push_back(op.top());
            op.pop();
        }
        return res;
    }
    
    int getRes(vector<string>& tokens){
        stack<int> st;
        for(int i = 0; i < tokens.size(); ++i){
            if(tokens[i] == "+"|| tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
                int num1 = st.top();
                st.pop();
                int num2 = st.top();
                st.pop();
                if(tokens[i] == "+") st.push(num2 + num1);
                if(tokens[i] == "-") st.push(num2 - num1);
                if(tokens[i] == "*") st.push(num2 * num1);
                if(tokens[i] == "/") st.push(num2 / num1);
            }else{
                // st.push(stoi(tokens[i]));
                stringstream ss(tokens[i]);
                int num;
                ss >> num;
                st.push(num);
            }
        }
        int res = st.top();
        st.pop();
        return res;
    }  

public:
    int calculate(string s) {
        string noBlackIn_s = removeBlack(s);
        vector<string> rpn4s = toRPN(noBlackIn_s);
        
        return getRes(rpn4s);
    }
};

放弃逆波兰表达式的写法了

改用栈吧，下面贴一个论坛老哥的解法的分析，我修不动原来的代码了

class Solution {
public:

    // 去除空格
    string removeBlank(string s) {
        string res = "";
        for(char c:s) {
            if(c!=' ') res += c;
        }
        return res;
    }

    // 将中缀表达式转化为后缀表达式
    queue<string> getToken(string s) {
        
        s = removeBlank(s);
        string push_src = "";
        queue<string> res;
        bool pre = true;
        for(char c:s) {
            //判断是不是单目运算符 使用$代替单目运算符
            if(c == '-' && pre) {
                if(push_src!="") {
                    res.push(push_src);
                    push_src = "";
                    
                }
                res.push("$");
                
            }else if(c == '+' || c=='-' || c=='*' || c=='/' || c=='(' || c==')'||c=='#') {
                if(c!=')')pre = true;
                if(push_src!="") {
                    res.push(push_src);
                    push_src = "";
                    
                }
                res.push(string("")+c);
            }else{
                pre = false;
                push_src += c;
            }
        }
        if(push_src!="") {
            res.push(push_src);
            push_src = "";
        }
        return res;
    } 

    // 给定一个后缀表达式，求其值
    int calculate(string s) {
        queue<string> in = getToken(s+"#"); // #表示计算结束
        map<string,int> isp = {
            {"#",0},{"(",1},{"*",5},{"/",5},{"+",3},{"-",3},{")",8},{"$",7}
        };
        map<string,int> icp = {
            {"#",0},{"(",8},{"*",4},{"/",4},{"+",2},{"-",2},{")",1},{"$",6}
        };

        queue<string> out; // 存储后缀表达式
        stack<string> stk; // 操作符栈
        stk.push("#");
        string ch = in.front();  // 取队首元素
        in.pop();
        while(stk.top()!="#"||ch!="#") { // 当操作符栈为空且队列已经空了之后才结束循环
            if(isp.find(ch)==isp.end()) { // 判断是否为数字，不是则直接加入后缀表达式
                out.push(ch);
                ch = in.front();
                in.pop();
                continue;
            }
            if(icp[ch] > isp[stk.top()]) { // 操作符优先级较低则直接加入栈中
                stk.push(ch);
                ch = in.front();
                in.pop();

            }else if(icp[ch] < isp[stk.top()]) { // 操作符优先级较高则弹出栈顶操作符加入后缀表达式
                out.push(stk.top());
                stk.pop();
            }else { // 相等则弹出栈顶的左括号或右括号
                stk.pop();
                if(ch!="#") {
                    ch = in.front();
                    in.pop();
                }
            }
        }
        stack<int> sk;// 存储数字的栈
        //TODO:逆波兰式子求解
        while(!out.empty()) {// 遍历后缀表达式求值
            string cur = out.front();
            out.pop();
            if(cur == "$") {// 处理单目运算符
                int a = sk.top();
                sk.pop();
                sk.push(-a);
            }else if(cur == "+") {
                int a2 = sk.top();
                sk.pop();
                int a1 = sk.top();
                sk.pop();
                sk.push(a1+a2);               
            }else if(cur == "-") {
                int a2 = sk.top();
                sk.pop();
                int a1 = sk.top();
                sk.pop();
                sk.push(a1-a2); 
            }else if(cur == "*") {
                int a2 = sk.top();
                sk.pop();
                int a1 = sk.top();
                sk.pop();
                sk.push(a1*a2); 
            }else if(cur == "/") {
                int a2 = sk.top();
                sk.pop();
                int a1 = sk.top();
                sk.pop();
                sk.push(a1/a2); 
            }else {
                sk.push(stoi(cur));
            }
        }
        return sk.top();
    }
};

上述代码实现的是一个基本的四则运算计算器，其核心思路是将中缀表达式转化为后缀表达式，再根据后缀表达式求值得到结果。这个过程可以概括为：（GPT生成）

1. 初始化两个栈，一个操作符栈stk和一个数字栈sk，初始化一个队列out用来存储后缀表达式；
2. 遍历中缀表达式，对于每个字符进行如下判断：
   • 如果是数字，直接入队out；
   • 如果是左括号，入栈stk；
   • 如果是右括号，弹出操作符栈中的元素并加入队列out，直到遇到左括号；注意：左右括号都不入队out；
   • 如果是操作符，则判断其与操作符栈顶元素的优先级关系，如果优先级高，则压入操作符栈，否则将操作符栈中的元素弹出，加入队列out，然后继续比较栈顶元素和当前操作符的优先级，直至当前操作符可以入栈；
3. 当遍历完中缀表达式后，如果操作符栈中还有元素，则将其全部依次弹出，并加入队列out；
4. 此时out中存储的就是后缀表达式，对其进行求值即可得到结果。

例如，对于中缀表达式"3+42/(1-5)#"，按照上述算法可得到后缀表达式"34215-/+"。具体过程如下：

1. 初始化操作符栈和队列out，将中缀表达式转化为一个字符数组arr；
2. 从左到右遍历arr，对于每个元素进行判断：
   • 当前元素是数字，直接加入out中；
   • 当前元素是'('，压入操作符栈中；
   • 当前元素是')'，弹出操作符栈中的元素并加入out，直至遇到'('；
   • 当前元素是运算符，比较其与操作符栈顶元素的优先级，如果优先级高，则将其压入操作符栈；否则，依次弹出操作符栈中的元素并加入out，直至当前运算符可以入栈；
3. 遍历完arr后，将操作符栈中的剩余元素全部弹出，并加入out；
4. 对out中的元素进行求值，得到最终结果11。

在代码的 removeBlank 函数中，采用了一个简单的遍历字符串的方式来去除空格。具体来说，将原字符串中非空格的字符依次加入一个新的字符串中即可。

在处理单目运算符时，则需要考虑到单目运算符和减号（二元运算符）的区别。我们可以通过一个 bool 变量 pre 来判断当前字符是否为单目运算符。具体来说，如果 pre 为 true，且当前字符为减号，则说明其为单目运算符；否则，当前字符为减号则表示其为二元操作符。当遇到单目运算符时，我们可以将其替换为 "$"，在后面进行求值时再做特殊处理即可。

另外，在这个函数中还使用了一个辅助变量 push_src 来存储当前正在处理的数字串。当遇到运算符或者结束符号 # 时，就将该数字串加入队列 res 中。同时，pre 的取值根据当前字符是不是右括号进行相应的修改。

括号展开+栈

这个是LeetCode的官方解法

class Solution {
public:
    int calculate(string s) {
        stack<int> ops; // 用于存储括号内的符号
        ops.push(1); // 先将符号入栈，初始为1

        int sign = 1; // 当前数字的符号，默认为正数

        int ret = 0; // 最终结果
        int n = s.length(); // 字符串长度
        int i = 0; // 当前遍历到字符串中的位置
        while (i < n) {
            if (s[i] == ' ') { // 空格直接跳过
                i++;
            } else if (s[i] == '+') { // 遇到加号，更新符号为栈顶的符号
                sign = ops.top();
                i++;
            } else if (s[i] == '-') { // 遇到减号，更新符号为栈顶的符号的相反数
                sign = -ops.top();
                i++;
            } else if (s[i] == '(') { // 遇到左括号，将当前符号入栈
                ops.push(sign);
                i++;
            } else if (s[i] == ')') { // 遇到右括号，弹出栈顶符号
                ops.pop();
                i++;
            } else { // 遇到数字，计算出完整的数字，并与当前符号相乘后累加到最终结果
                long num = 0;
                while (i < n && s[i] >= '0' && s[i] <= '9') {
                    num = num * 10 + s[i] - '0';
                    i++;
                }
                ret += sign * num;
            }
        }
        return ret; // 返回最终结果
    }
};

上述代码基于栈的思想实现了对带有括号的数学表达式的计算。其核心思路如下：

? 1.使用一个操作符栈 ops 存储括号内的符号，初始时将 1 入栈表示整个表达式的符号为正号。

? 2.遍历表达式中的每个字符，分别处理以下几种情况：

? 如果遇到空格，直接跳过。

? 如果遇到加号 +，则更新当前符号为栈顶的符号，并继续向后遍历。

? 如果遇到减号 -，则更新当前符号为栈顶的符号的相反数，并继续向后遍历。

? 如果遇到左括号 (，则将当前符号入栈，并继续向后遍历。

? 如果遇到右括号 )，则弹出栈顶符号，并继续向后遍历。

? 如果遇到数字，则计算出完整的数字，并与当前符号相乘后累加到最终结果，并继续向后遍历。

? 3.最终返回最终结果即可。

这样的实现可以处理带有括号的复杂表达式，同时也考虑到了符号的影响。

举一个例子，计算表达式 "1 + (2 - 3) - 4"

首先初始化操作符栈 ops，将符号 1 入栈：ops: [1]

然后从左到右遍历表达式中的每个字符，依次进行处理：

? 遇到数字 1，累加到最终结果 ret 中，此时 ret=1。

? 遇到空格，直接跳过。

? 遇到加号 +，更新当前符号为 ops 栈顶的符号 1，此时 sign=1，继续向后遍历。

? 遇到左括号 (，将当前符号 sign=1 入栈，此时 ops: [1, 1]，继续向后遍历。

? 遇到数字 2，由于此时栈顶符号为正号，所以累加到最终结果 ret 中，此时 ret=3。

? 遇到减号 -，更新当前符号为栈顶的符号的相反数 -1，此时 sign=-1，继续向后遍历。

? 遇到数字 3，由于此时栈顶符号为负号，所以将其乘以 (-1) 并累加到最终结果 ret 中，此时 ret=2。

? 遇到右括号 )，弹出栈顶符号，并继续向后遍历，此时 ops: [1]。

? 遇到减号 -，更新当前符号为栈顶的符号的相反数 -1，此时 sign=-1，继续向后遍历。

? 遇到数字 4，由于此时栈顶符号为负号，所以将其乘以 (-1) 并累加到最终结果 ret 中，此时 ret=-3。

最终返回结果 ret=-3