深度学习入门系列之doc

这周老师让把深度学习的名词过一遍，小玛同学准备在过一遍Deep Learning名词的同时把基本的模型也过一遍。
感谢杰哥发我深度学习入门系列能让我有机会快速入门。
下面就来doc一些学到的东西

线性感知器

感知器（线性单元）有个问题就是当面对的数据集不是线性可分的时候，“感知器规则”可能无法收敛，这意味着我们永远无法完成一个感知器的训练。（即如果我们需要用感知器（神经元）拟合的映射不是线性的，那么需要用在拟合中添加非线性的函数）

SGD vs BGD

SGD: Stochastic Gradient Descent
BGD: Batch Gradient Descent
SGD 和 BGD 之间的主要区别在于每次迭代的更新步骤。BGD 在每一步都使用整个数据集计算梯度，而 SGD 在每一步都使用单个样本或一小批样本计算梯度。这使得 SGD 比 BGD 更快，计算成本更低。
然而，在凸集中，由于其随机性质，SGD 可能永远无法达到全局最小值，而是不断在接近全局最小值的区域内游荡。另一方面，BGD 只要有足够的时间和合适的学习率，就能保证找到全局最小值。
但是在非凸集中，随机性有助于我们逃离一些糟糕的局部最小值。

感知器 vs 神经元

一般情况下，说感知器的时候，它的激活函数是阶跃函数；当我们说神经元的时候，激活函数往往选择为sigmoid函数或者是tanh函数。

sigmoid函数

sigmoid函数的导数非常有趣，它可以用sigmoid函数自身来表示。这样，一旦计算出sigmoid函数的值，计算它的导数的值就非常方便。
令 \(y = sigmoid(x)\) , 则 \(y^{\prime} = y(1 ? y)\)

梯度检查

下面是梯度检查的代码。如果我们想检查参数 的梯度是否正确，我们需要以下几个步骤：

1. 首先使用一个样本 \(d\) 对神经网络进行训练，这样就能获得每个权重的梯度。
2. 将 \(w_{ji}\) 加上一个很小的值( \(10^{-4}\) )，重新计算神经网络在这个样本 \(d\) 下的 \(E_{d+}\)。
3. 将 \(w_{ji}\) 减上一个很小的值( \(10^{-4}\) )，重新计算神经网络在这个样本 \(d\) 下的 \(E_{d-}\) 。
4. 根据下面的公式计算出期望的梯度值，和第一步获得的梯度值进行比较，它们应该几乎想等(至少4位有效数字相同)。

\[\frac{\partial E_d(w_{ji})}{\partial w_{ji}} \approx \frac{f(w_{ji} + \epsilon) - f(w_{ji} - \epsilon)}{2\epsilon} \]

当然，我们可以重复上面的过程，对每个权重 \(w_{ji}\) 都进行检查。也可以使用多个样本重复检查。

卷积神经网络

CNN 更适合图像，语音识别任务，它儿孙辈的人才包括谷歌的GoogleNet、微软的ResNet。

梯度消失问题

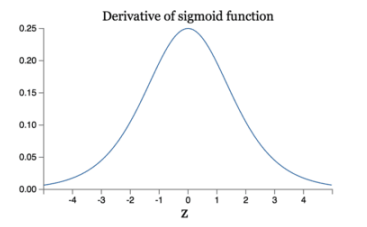
减轻梯度消失问题 回忆一下计算梯度的公式 \(\nabla = \sigma^{\prime}\delta x\) 。其中，\(\sigma^{\prime}\) 是sigmoid函数的导数。在使用反向传播算法进行梯度计算时，每经过一层
sigmoid神经元，梯度就要乘上一个 \(\sigma^{\prime}\) 。从下图可以看出，\(\sigma^{\prime}\) 函数最大值是1/4。因此，乘一个 \(\sigma^{\prime}\) 会导致梯度越来越小，这对于深层网络的训练是个很大的问题。

ReLU 函数的优势

Relu函数作为激活函数，有下面几大优势：

1. 速度快 和sigmoid函数需要计算指数和倒数相比，relu函数其实就是一个max(0,x)，计算代价小很多。
2. 减轻梯度消失问题 而relu函数的导数是1，不会导致梯度变小。当然，激活函数仅仅是导致梯度减小的一个因素，但无论如何在这方面relu的表现强于sigmoid。使用relu激活函数可以让你训练更深的网络。
3. 稀疏性 通过对大脑的研究发现，大脑在工作的时候只有大约5%的神经元是激活的，而采用sigmoid激活函数的人工神经网络，其激活率大约是50%。有论文声称人工神经网络在15%-30%的激活率时是比较理想的。因为relu函数在输入小于0时是完全不激活的，因此可以获得一个更低的激活率。

卷积神经网络的实现

三大要点：

1. 局部连接
2. 权值共享
3. 下采样 可以使用Pooling来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

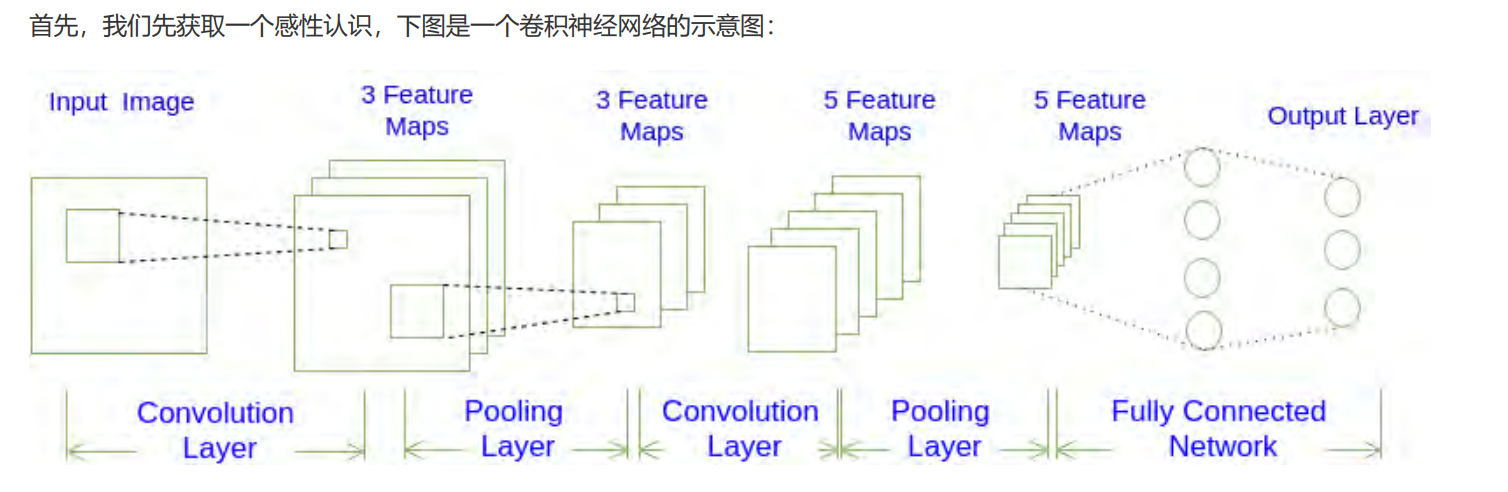
如图所示，一个卷积神经网络由若干卷积层、Pooling 层、全连接层组成。你可以构建各种不同的卷积神经网络，它的常用架构模式为：

\[INPUT -> [[CONV]*N -> POOL ] * M -> [FC] * K \]

也就是N个卷积层叠加，然后(可选)叠加一个Pooling层，重复这个结构M次，最后叠加K个全连接层。
对于图展示的卷积神经网络：

\[INPUT -> CONV -> POOL -> CONV -> POOL -> FC -> FC \]

按照上述模式可以表示为：

\[INPUT -> [[CONV]*1 -> POOL]*2 -> [FC]*2 \]

也就是：$$N=1, M=2, K=2$$。
三维的层结构
从图1我们可以发现卷积神经网络的层结构和全连接神经网络的层结构有很大不同。全连接神经网络每层的神经元是按照一维排列的，也就是排成一条线的样子；而卷积神经网络每层的神经元是按照三维排列的，也就是排成一个长方体的样子，有宽度、高度和深度。
对于图1展示的神经网络，我们看到输入层的宽度和高度对应于输入图像的宽度和高度，而它的深度为1。接着，第一个卷积层对这幅图像进行了卷积操作(后面我们会讲如何计算卷积)，得到了三个Feature Map。这里的"3"可能是让很多初学者迷惑的地方，实际上，就是这个卷积层包含三个Filter，也就是三套参数，每个Filter都可以把原始输入图像卷积得到一个Feature Map，三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter，那是可以自由设定的。也就是说，卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征，三个Filter就对原始图像提取出三组不同的特征，也就是得到了三个Feature Map，也称做三个通道(channel) 。
继续观察图1，在第一个卷积层之后，Pooling层对三个Feature Map做了下采样(后面我们会讲如何计算下采样)，得到了三个更小的FeatureMap。接着，是第二个卷积层，它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map 卷积在一起，得到一个新的Feature Map 。这样，5个Filter 就得到了5个Feature Map 。接着，是第二个Pooling ，继续对5个Feature Map 进行下采样，得到了5个更小的Feature Map。
图1所示网络的最后两层是全连接层。第一个全连接层的每个神经元，和上一层5个Feature Map中的每个神经元相连，第二个全连接层(也就是输出层)的每个神经元，则和第一个全连接层的每个神经元相连，这样得到了整个网络的输出。