一致性hash算法原理及实践

大家好，我是蓝胖子，想起之前学算法的时候，常常只知表面，不得精髓，这个算法到底有哪些应用场景，如何应用在工作中，后来随着工作的深入，一些不懂的问题才慢慢被抽丝剥茧分解出来。

今天我们就来看看工作和面试中经常被点名的算法，一致性hash算法，并且我会介绍它在实际的应用场景并用代码实现出来。

本节的源码已经上传到github

https://github.com/HobbyBear/codelearning/tree/master/consistenthash

原理介绍

首先我们来看看一致性hash的定义和算法思想，一致性hash算法有别于传统hash算法，例如我们有3个节点，现在要考虑某个key值落到哪个节点上，传统hash算法是将key通过hash函数后通过节点数量进行取模运算得到需要落到的节点序号。

nodeIdx := hashFunc(key)%len(nodes)

传统hash算法在节点数量变化时基本上会导致大量旧数据经过hash得到的节点序号失效， 而一致性hash算法则能够保证只有少部分旧数据需要重新改变需要落到的节点，其余数据依然能够保证节点扩容后，hash计算得到的节点序号和之前一致。

一致性hash算法假设了一个很大的数字空间，比如2的32次方， 节点信息会被映射到这个数字空间的某个数字上，当我们需要看某个key落到哪个节点上时，也需要将key进行hash计算得到某个数字，接着就是找到在这个超大数字空间内，第一个大于该数字的节点。如果没有大于该数字的节点，则将第一个节点作为key需要落到的节点。

这样就等效于整个数字空间构成了一个环形结构，寻找key需要落到的节点上时，则是从key开始顺时针寻找第一个节点。

用下面的示意图来表示这个过程会更好理解

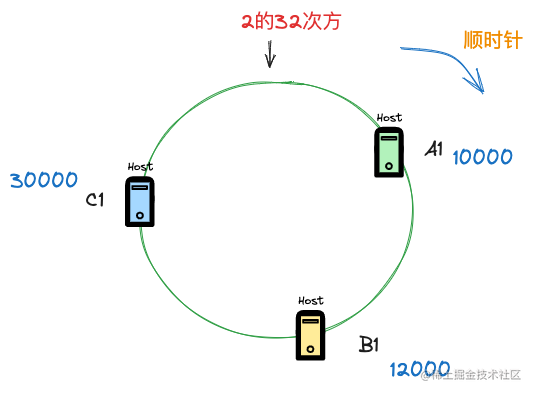
我们假设有3个节点A1,B1,C1, 这三个节点的信息(比如主机名，ip等信息)经过hash运算后得到了3个数字，A1对应10000，B1对应12000，C1 对应30000，现在需要看某个key需要落到哪个节点上，就应该这样来看。

注意这里的节点我是拿服务器来举例，实际上，节点也可以是表，某个key可以看出是表中的某一行，而一致性性hash算法的目的则是看某一行数据应该落到哪个表中，总之你可以发挥你的想象将算法中的事物进行代替抽象，算法的思想终究是不变的。

当某个key经过hash计算后，得到数字9000，那么在顺时针寻找到第一个大于它的节点则是节点A1,如果key经过hash计算后，得到数字11000，那么寻找到的第一个大于它的节点则是节点B1。 注意一种特殊情况，如果key经过hash计算得到的数字是40000，那么此时没有任何一个节点是大于这个数字的，这种情况，正如上图所示，一致性hash算法的数组空间是环形结构，这样key会落到第一个节点A1上。

这个只是最初版本的一致性hash，它会在节点数量较少时，出现分配数据不均匀的情况，比如可能会出现下面的场景

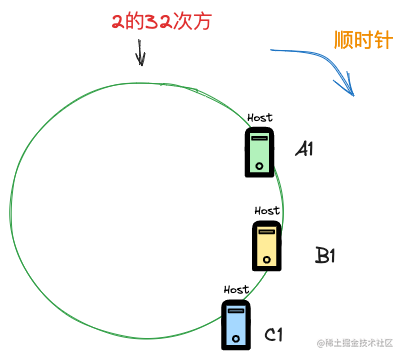
所有的节点都偏向了一侧，这样将会有大量数据落到A1 节点，造成数据分配不均匀。

所以一致性hash算法的改进版本提出虚拟节点的概念，通过引入节点的副本来让整个hash环上的节点数量多起来。

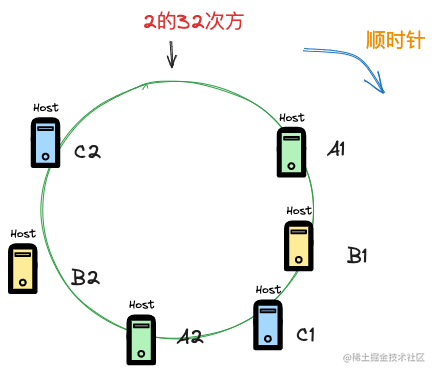
这里假设引入的副本是一个，那么参与分配的key的节点在hash环上则是6个，6个节点会让对hash环的分配更加均匀，注意虚拟节点在实际环境中并不存在，比如这里虚拟节点A2和实际的节点A1指向的其实都是同一个实际环境中的节点。

应用场景

在了解了一致性hash算法的原理后，我们再来看看它的一些适用场景，这样能够明白算法的目的，不至于纸上谈兵。

负载均衡

首先来看下第一种应用场景，在负载均衡中的应用，拿memcache举例，memcache的分布式架构其实是依赖客户端来实现的，客户端将缓存key通过一致性hash算法计算需要缓存到哪台后端服务器上。

而采用一致性hash的好处则是在扩缩容时，不会导致大面积的缓存失效。

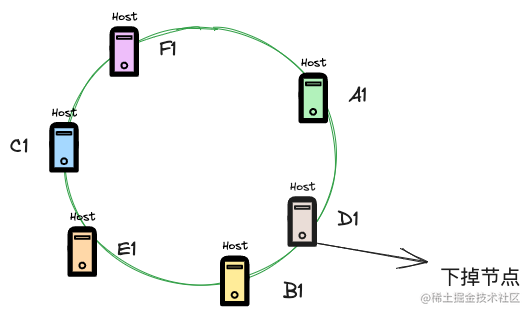
如上图所示，现在要将D1节点下掉，由于一致性hash算法路由节点是顺时针的，那么只会影响到D1和A1之间的数据，这部分数据后续需要在B1节点上进行读取，而其他节点上的数据则不会影响。

其实，从这里应该能够看出，一致性hash算法在负载均衡中一个极大的好处就是，对于有状态的服务，能够做到扩缩容节点时，影响面最小。

分库分表

再来看看在分库分表中的应用，如果分表时采用传统hash算法，当还想扩容表时，不得不面对对所有分表数据进行重新hash，重新写入，这无论是对于磁盘io还是cpu都有极大的压力，我们应该在新增分表时尽量迁移少量的数据，减少影响面，这不正是一致性hash算法的功能吗。

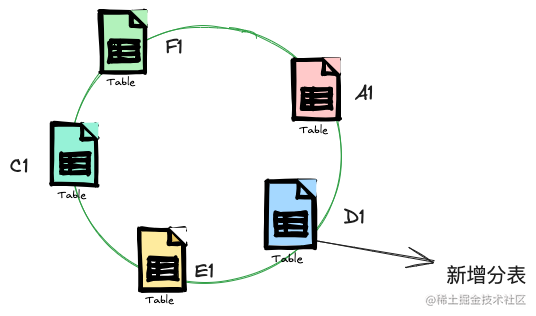
如上图所示，现在新增了分表D1，那么会影响到之前D1到A1的之前的数据，这部分数据之前是存到E1这张表上的，现在要迁移到D1表，所以你可以看到新增一个分表只会设计两张表部分数据的迁移，相比传统hash的全量迁移，优势不言而喻。

代码实现

现在我们来看下如何实现下这个算法。

我们需要将节点信息以及用户key信息映射成一个数字，这里要用到hash函数，hash函数有很多，我们直接用一个，crc32的hash方式，这样返回的数字刚好在2的32次方以内。

func ChecksumIEEE(data []byte) uint32 

同时我们需要一个映射结构存储节点在环上的hash key与节点信息，还需要一个有序列表存储hash key，以便于查询用户key对应的节点hash key是哪一个。

这里的代码比较简单，短短20多行即可。

package main  
  
import (  
   "fmt"  
   "hash/crc32"  
    "sort")  
  
func main() {  
   ch := NewConsistentHash(3)  
   ch.AddNodes("node1")  
   ch.AddNodes("node2")  
   ch.AddNodes("node3")  
   fmt.Println(ch.GetNode("lanpangzi"))  
}  
  
type ConsistentHash struct {  
   nodes      map[uint32]string  
   keys       []uint32  
   replicates int  
}  
  
func NewConsistentHash(replicate int) *ConsistentHash {  
   return &ConsistentHash{  
      nodes:      make(map[uint32]string),  
      keys:       make([]uint32, 0),  
      replicates: replicate,  
   }  
}  

func (c *ConsistentHash) AddNodes(node string) {  
   for i := 0; i <= c.replicates; i++ {  
      nodename := fmt.Sprintf("%s%d", node, i)  
      hashKey := crc32.ChecksumIEEE([]byte(node))  
      c.nodes[hashKey] = nodename  
      c.keys = append(c.keys, hashKey)  
   }  
   sort.Slice(c.keys, func(i, j int) bool {  
      return c.keys[i] < c.keys[j]  
   })  
}  

func (c *ConsistentHash) GetNode(key string) string {  
   hashKey := crc32.ChecksumIEEE([]byte(key))  
   nodekeyIndex := sort.Search(len(c.keys), func(i int) bool {  
      return c.keys[i] >= hashKey  
   })  
   if nodekeyIndex == len(c.keys) {  
      nodekeyIndex = 0  
   }  
   return c.nodes[c.keys[nodekeyIndex]]  
}

我们搞定了一致性hash算法，代码实现并不难，关键是要搞懂算法的原理以及作用，这样才能灵活运用。